05-Python整数的底层实现

05-Python整数的底层实现

这次我们来分析一下Python中的整数是如何实现的，我们知道Python中的整数是不会溢出的，换句话说，它可以计算无穷大的数。只要你的内存足够，它就能计算，但是对于C来说显然是不行的，可Python底层又是C实现的，那么它是怎么做到整数不会溢出的呢？

既然想知道答案，那么看一下Python中的整型在底层是怎么定义的就行了。

int实例对象的底层实现

Python中的整数底层对应的结构体是PyLongObject，它位于longobject.h中。

//longobject.h
typedef struct _longobject PyLongObject; /* Revealed in longintrepr.h */

//longintrepr.h
struct _longobject {
    PyObject_VAR_HEAD
    digit ob_digit[1];
};

//合起来可以看成
typedef struct {
    PyObject_VAR_HEAD
    digit ob_digit[1];
} PyLongObject;

//如果把这个PyLongObject更细致的展开一下就是
typedef struct {
    Py_ssize_t ob_refcnt; //引用计数
    struct _typeobject *ob_type; //类型
    Py_ssize_t ob_size; //维护的元素个数
    digit ob_digit[1]; //digit类型的数组,长度为1
} PyLongObject;

别的先不说，就冲里面的ob_size我们就可以思考一番。首先Python中的整数有大小、但应该没有长度的概念吧，那为什么会有一个ob_size呢？从结构体成员来看，这个ob_size指的应该就是ob_digit数组的长度，而这个ob_digit数组显然只能是用来维护具体的值了。而数组的长度不同，那么对应的整数占用的内存也不同。所以答案出来了，整数虽然没有我们生活中的那种长度的概念，但它是个变长对象，因为不同的整数占用的内存可能是不一样的。

因此这个ob_size它指的是底层数组的长度，因为Python中整数对应的值在底层是使用数组来存储的。尽管它没有字符串、列表那种长度的概念，或者说无法对整型使用len方法，但它是个变长对象。

​ 那么下面的重点就在这个ob_digit数组了，我们要从它的身上挖掘信息，看看Python中整数对应的值(比如123)，是怎么放在这个数组里面的。不过首先我们要看看这个digit是个什么类型，它同样定义在longintrepr.h中

//PYLONG_BITS_IN_DIGIT是一个宏，如果你的机器是64位的，那么它会被定义为30，32位机器则会被定义为15
//至于这个宏是做什么的我们先不管
#if PYLONG_BITS_IN_DIGIT == 30
typedef uint32_t digit;
// ...
#elif PYLONG_BITS_IN_DIGIT == 15
typedef unsigned short digit;
// ...
#endif

而我们的机器现在基本上都是64位的，所以PYLONG_BITS_IN_DIGIT会等于30，因为digit等价于uint32_t(unsigned int)，所以它是一个无符号32位整型。

所以ob_digit这个数组是一个无符号32位整型数组，长度为1。当然这个数组具体多长则取决于你要存储的Python整数有多大，因为C中数组的长度不属于类型信息，你可以看成是长度n，而这个n是多少要取决于你的整数大小。显然整数越大，这个数组就越长，那么占用空间就越大。

​ 搞清楚了PyLongObject里面的所有成员，那么下面我们就来分析ob_digit是怎么存储Python中的整数，以及Python中的整数为什么不会溢出。

​ 不过说实话，关于Python的整数不会溢出这个问题，其实相信很多人已经有答案了，因为底层是使用数组存储的嘛，而数组的长度又没有限制，所以当然不会溢出啦。

​ 另外，还存在一个问题，那就是digit是一个无符号32位整型，那负数怎么存储？别着急，我们会举栗说明，将上面的疑问一一解答。

首先如果你是Python的设计者，要保证整数不会溢出，你会怎么办？我们把问题简化一下，假设有一个8位的无符号整数类型，我们知道它能表示的最大数字是255，但这时候如果我想表示256，要怎么办？

可能有人会想，那用两个数来存储不就好了。一个存储255，一个存储1，将这两个数放在数组里面。这个答案的话，虽然有些接近，但其实还有很大偏差：那就是我们并不能简单地按照大小拆分的，256拆分为255和1，要是265就拆分成255和10，而是要通过二进制的方式，我们来简单看一下。

我们知道8位整数最大就是 2 ^ 8 - 1,也就是它的八位全部都是1,结果是255
所以255对应的数组就是: [255], 因为此时一个8位整数就能存下

但如果是256,那么8位显然存不下了,此时就还需要一个位
所以这个时候会使用两个8位整数, 但并不是简单的相加, 而是使用一个新的8位整数来模拟更高的位

​ 而Python底层也是类似这种做法，但是考虑的会更加全面。下面就以Python中的整数为例，看看底层数组的存储方式。

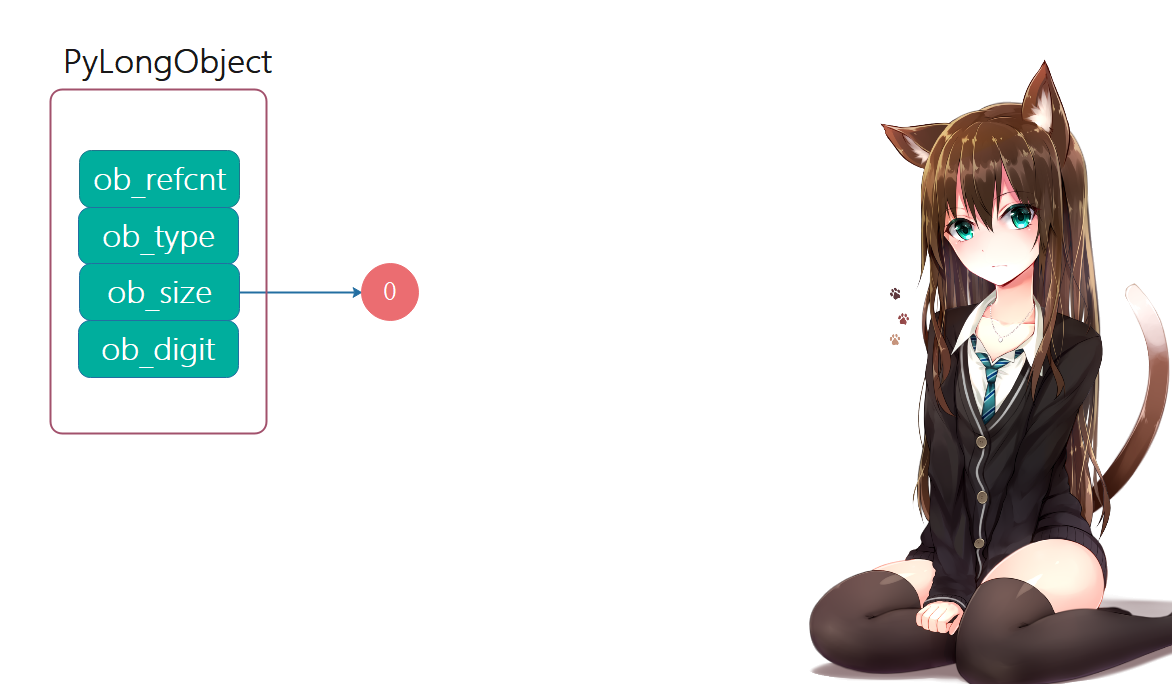
整数0：

注意：当要表示的整数为0时，ob_digit这个数组为空，不存储任何值，ob_size为0，表示这个整数的值为0，这是一种特殊情况。

整数1：

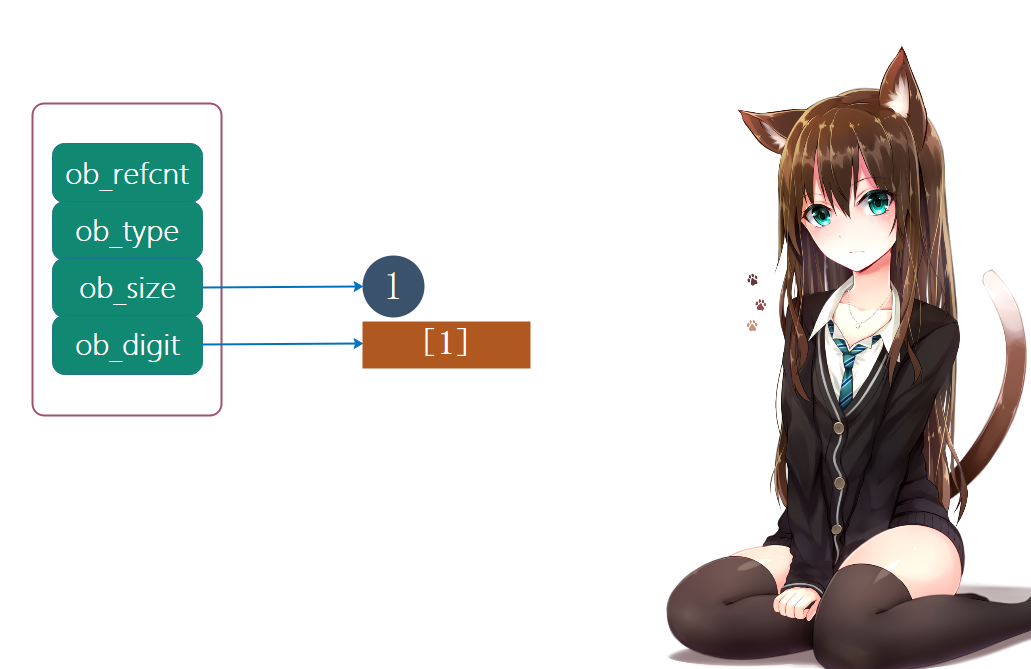
当然存储的值为1时，ob_size的值就是1，此时ob_digit数组就是[1]。

整数-1：

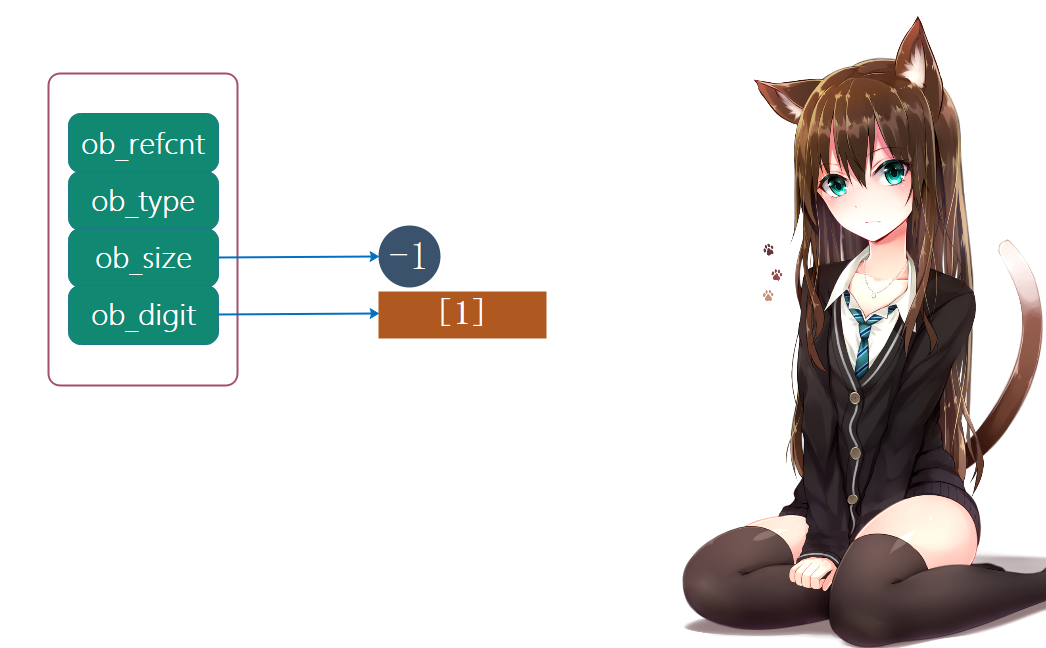
我们看到ob_digit数组没有变化，但是ob_size变成了-1，没错，整数的正负号是通过这里的ob_size决定的。ob_digit存储的其实是绝对值，无论n取多少，-n和n对应的ob_digit是完全一致的，但是ob_size则互为相反数。所以ob_size除了表示数组的长度之外，还可以表示对应整数的正负。

所以我们之前说整数越大，底层的数组就越长。更准确的说是绝对值越大，底层数组就越长。所以Python在比较两个整型的大小时，会先比较ob_size，如果ob_size不一样则可以直接比较出大小来。显然ob_size越大，对应的整数越大，不管ob_size是正是负，都符合这个结论，可以想一下。

整数2 ^ 30 -1：

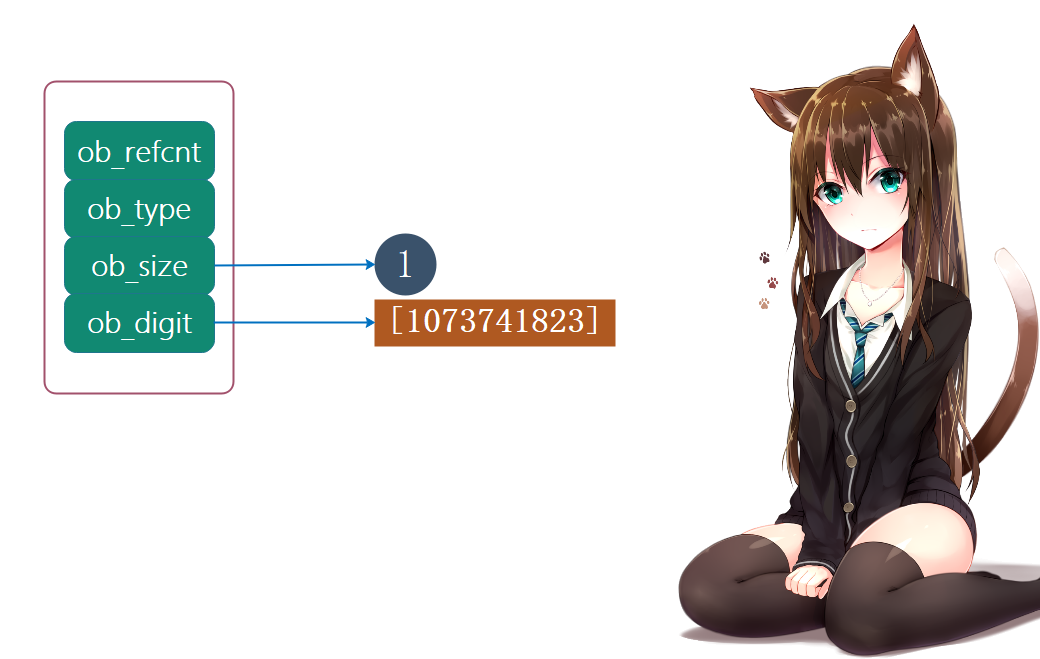
如果想表示2 ^30 - 1(^这里代指幂运算,当然对于Python程序猿来说两个星号也是幂运算,表达的意义是一样的)，那么也可以使用一个digit表示。虽然如此，但为什么突然举2 ^ 30 - 1这个数字呢？答案是，虽然digit是4字节、32位，但是Python只用30个位。

之所以这么做是和加法进位有关系，如果32个位全部用来存储其绝对值，那么相加产生进位的时候，可能会溢出，比如有一个将32个位全部占满的整数(2 ^ 32 - 1)，即便它只加上1，也会溢出。这个时候为了解决这个问题，就需要先强制转换为64位再进行运算。

但如果只用30个位的话，那么加法是不会溢出的，或者说相加之后依旧可以用32位整数保存。因为30个位最大就是2 ^ 30 - 1，即便两个这样的值相加，结果也是(2 ^ 30 - 1) * 2，即：2 ^ 31 - 2。而32个位的话最大是2 ^ 32 - 1，所以肯定不会溢出的；如果一开始30个位就存不下，那么数组中会有两个digit。

所以虽然将32位全部用完，可以只用一个digit表示更多、更大的整数，但是可能面临相加之后一个digit存不下的情况，于是只用30个位，如果数值大到30个位存不下的话，那么就会多使用一个digit。可能有人发现了，如果是用31个位的话，那么相加产生的最大值就是2 ^ 32 - 2，结果依旧可以使用一个32位整型存储啊，那Python为啥要牺牲两个位呢？答案是为了乘法运算。

// 还记得这个宏吗？PYLONG_BITS_IN_DIGIT指的就是Python使用digit的位数
// 我们看到在32位机器上，digit相当于2字节、16位的整型，而它用了15位，只牺牲了一个位
// 64 位机器上则牺牲两个位
#if PYLONG_BITS_IN_DIGIT == 30
typedef uint32_t digit;
// ...
#elif PYLONG_BITS_IN_DIGIT == 15
typedef unsigned short digit;
// ...
#endif

整数2 ^ 30：

问题来了，我们说digit只用30位，所以2 ^ 30 - 1是一个digit能存储的最大值，那么现在是2 ^ 30，所以数组中就要有两个digit了。

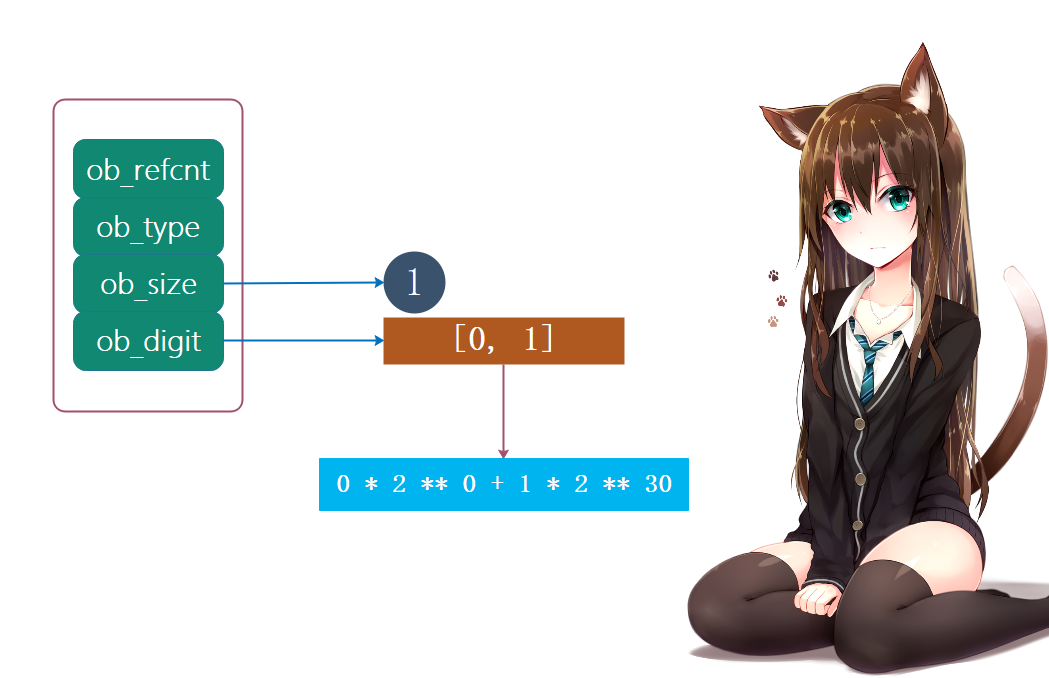
我们看到此时就用两个digit来存储了，此时的数组里面的元素就是0和1，而且充当高位的放在后面，因为我们说了使用新的digit来模拟更高的位。由于一个digit只用30位，那么数组中第一个digit的最低位就是1，第二个digit的最低位就是31，第三个digit的最低位就是61，以此类推，所以如果ob_digit为[a, b, c]，那么对应的整数就为: a * 2 * 0 + b * 2 * 30 + c * 2 ** 60，如果ob_digit不止3个，那么就按照30个位往上加，比如ob_digit还有第四个元素d，那么就再加上d * 2 ** 90即可。**

再比如我们反推一下，如果a = 88888888888，那么底层数组ob_digit中的值是多少？

import numpy as np

a = 88888888888
# 我们说1个digit用30个位, 那么n个digit所能表示的最大整数就是2 ** (30 * n) - 1, 至于原因的话其实很好理解，但我们还是可以严格推导一下
# 我们以n = 2为例, 显然两个digit最高能表示 (2 ** 30 - 1) + (2 ** 30 - 1) * 2 ** 30,
# 它等于 (2 ** 30 - 1) + (2 ** 60 - 2 ** 30) = 2 ** 60 - 1, 因此两个digit最大可以表示 2 ** 60 - 1
# 同理你可以n取3, 看看(2 ** 30 - 1) + (2 ** 30 - 1) * 2 ** 30 + (2 ** 30 - 1) * 2 ** 60是不是等于2 ** 90 - 1
# 或者试试更大的数, 结论都是成立的
print(np.log2(a))  # 36.37128404230425
# 36超过了30个位、但小于90个位, 因此需要两个digit

# 我们说 "整数 = ob_digit[0] + ob_digit[1] * 2 ** 30 + ob_digit[2] * 2 ** 60 + ..."
# 但是对于ob_digit长度为2的情况下, 这里的a = ob_digit[0] + ob_digit[1] * 2 ** 30
print(a // 2 ** 30)  # 82
print(a - 82 * 2 ** 30)  # 842059320

# 说明此时底层对应的ob_digit数组就是[842059320, 82]

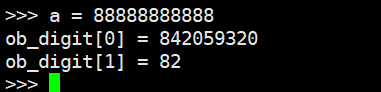
我们修改解释器源代码重新编译，通过在创建整数的时候打印ob_digit里面的元素的值，也印证了这个结论。

​ 这个时候，我们可以分析整数所占的字节了。相信所有人都知道可以使用sys.getsizeof计算大小，但是这大小到底是怎么来的，估计会一头雾水。因为Python中对象的大小，是根据底层的结构体计算出来的。

​ 我们说ob_refcnt、ob_type、ob_size这三个是整数所必备的，它们都是8字节，加起来24字节。所以任何一个整数所占内存都至少24字节，至于具体占多少，则取决于ob_digit里面的元素都多少个。

​ 因此Python中整数所占内存 = 24 + 4 * ob_digit数组长度

import sys

# 如果是0的话, ob_digit数组为空, 所以此时就是24字节
print(sys.getsizeof(0))  # 24

# 如果是1的话, ob_digit数组有一个元素, 所以此时是24 + 4 = 28字节
print(sys.getsizeof(1))  # 28
print(sys.getsizeof(2 ** 30 - 1))  # 28

# 一个digit只用30位, 所以最大能表示2 ** 30 - 1
# 如果是2 ** 30, 那么就需要两个元素, 所以是24 + 4 * 2 = 32字节
# 如果是两个digit, 那么能表示的最大整数就是2 ** 60 - 1
print(sys.getsizeof(2 ** 30))  # 32
print(sys.getsizeof(2 ** 60 - 1))  # 32


"""
相信下面的不需要解释了
"""
print(sys.getsizeof(1 << 60))  # 36
print(sys.getsizeof((1 << 90) - 1))  # 36

print(sys.getsizeof(1 << 90))  # 40

小整数对象池

由于分析过了浮点数以及浮点类型对象，因此int类型对象的实现以及int实例对象的创建啥的就不说了，可以自己去源码中查看，我们后面会着重介绍它的一些操作。还是那句话，Python中的API设计的很优美，都非常的相似，比如创建浮点数可以使用PyFloat_FromDouble、PyFloat_FromString等等，那么创建整数也可以使用PyLong_FromLong、PyLong_FromDouble、PyLong_FromString等等，直接去Objects中对应的源文件中查看即可。

这里说一下Python中的小整数对象池，我们知道Python中的整数属于不可变对象，运算之后会创建新的对象。

>>> a = 666
>>> id(a)
2431274354736
>>> a += 1
>>> id(a)
2431274355024
>>>

所以这种做法就势必会有性能缺陷，因为程序运行时会有大量对象的创建和销毁。根据浮点数的经验，我们猜测Python应该也对整数使用了缓存池吧。答案是差不多，只不过不是缓存池，而是小整数对象池

Python将那些使用频率高的整数预先创建好，而且都是单例模式，这些预先创建好的整数会放在一个静态数组里面，我们称为小整数对象池。如果需要使用的话会直接拿来用，而不用重新创建。注意：这些整数在Python解释器启动的时候，就已经创建了。

小整数对象池的实现位于longobject.c中。

#ifndef NSMALLPOSINTS
#define NSMALLPOSINTS           257
#endif
#ifndef NSMALLNEGINTS
#define NSMALLNEGINTS           5
#endif

static PyLongObject small_ints[NSMALLNEGINTS + NSMALLPOSINTS];

• NSMALLPOSINTS宏规定了对象池中正数的个数 (从 0 开始，包括 0 )，默认 257 个；
• NSMALLNEGINTS宏规定了对象池中负数的个数，默认5个；
• small_ints是一个整数对象数组，保存预先创建好的小整数对象；

以默认配置为例，Python解释器在启动的时候就会预先创建一个可以容纳262个整数的数组，并会依次初始化 -5 到 256(包括两端)之间的262个PyLongObject。所以小整数对象池的结构如下：

但是为什么要实现缓存从-5到256之间的整数呢？因为Python认为这个范围内的整数使用频率最高，而缓存这些整数的内存相对可控。因此这只是某种权衡，很多程序的开发场景都没有固定的正确答案，需要根据实际情况来权衡利弊。

>>> a = 256
>>> b = 256
>>> id(a), id(b)
(140714000246400, 140714000246400)
>>>
>>> a = 257
>>> b = 257
>>> id(a), id(b)
(2431274355184, 2431274354896)
>>>

256位于小整数对象池内，所以全局唯一，需要使用的话直接去取即可，因此它们的地址是一样的。但是257不再小整数对象池内，所以它们的地址不一样。

我们上面是在交互式下演示的，但如果有小伙伴不是通过交互式的话，那么会得到出乎意料的结果。

a = 257
b = 257
print(id(a) == id(b))  # True

可能有人会好奇，为什么地址又是一样的了，257明明不在小整数对象池中啊。虽然涉及到了后面的内容，但是提前解释一下也是可以的。主要区别就在于一个是在交互式下执行的，另一个是通过 python3 xxx.py的方式执行的。

首先Python的编译单元是函数，每个函数都有自己的作用域，在这个作用域中出现的所有常量都是唯一的，并且都位于常量池中，由co_consts指向。虽然我们上面的不是函数，而是在全局作用域中，但是全局你也可以看成是一个函数，它也是一个独立的编译单元。同一个编译单元中，常量只会出现一次。

当a = 257的时候，会创建257这个整数、并放入常量池中；所以b = 257的时候就不会再创建了，因为常量池中已经有了，所以会直接从常量池中获取，因此它们的地址是一样的，因为是同一个PyLongObject。

# Python3.6下执行, 该系列的所有代码都是基于Python3.8, 但是这里先使用Python3.6, 至于原因, 后面会说
def f1():
    a = 256
    b = 257
    return id(a), id(b)


def f2():
    a = 256
    b = 257
    return id(a), id(b)


print(f1())  # (140042202371968, 140042204149712)
print(f2())  # (140042202371968, 140042204255024)

此时f1和f2显然是两个独立的编译单元，256属于小整数对象池中的整数、全局唯一，因此即便不在同一个编译单元的常量池中，它的地址也是唯一的，因为它是预先定义好的，所以直接拿来用。但是257显然不是小整数对象池中的整数，而且不在同一个编译单元的常量池中，所以地址是不一样的。

而对于交互式环境来说，因为我们输入一行代码就会立即执行一行，所以任何一行可独立执行的代码都是一个独立的编译单元。注意：是可独立执行的代码，比如变量赋值、函数、方法调用等等；但如果是if、for、while、def等等需要多行表示的话，比如：if 2 > 1:，显然这就不是一行可独立执行的代码，它还依赖你输入的下面的内容。

>>> if 2 > 1:  # 此时按下回车，我们看到不再是>>>, 而是..., 代表还没有结束, 还需要你下面的内容
...     print("2 > 1")
...  # 此时这个if语句整体才是一个独立的编译单元
2 > 1
>>>

但是像a = 1、foo()、lst.appned(123)这些显然它们是一行可独立执行的代码，因此在交互式中它们是独立的编译单元。

>>> a = 257  # 此时这行代码已经执行了，它是一个独立的编译单元
>>> b = 257  # 这行代码也是独立的编译单元，所以它里面的常量池为空，因此要重新创建
>>> id(a), id(b)  # 由于它们是不同常量池内的整数，所以id是不一样的。
(2431274355184, 2431274354896)

但是问题来了，看看下面的代码，a和b的地址为啥又一样了呢？666和777明显也不在常量池中啊。

>>> a = 666;b=666
>>> id(a), id(b)
(2431274354896, 2431274354896)
>>> a, b = 777, 777
>>> id(a), id(b)
(2431274354800, 2431274354800)
>>>

显然此时应该已经猜到原因了，因为上面两种方式无论哪一种，都是在同一行，因此整体会作为一个编译单元，所以地址是一样的。

def f1():
    a = 256
    b = 2 ** 30
    return id(a), id(b)


def f2():
    a = 256
    b = 2 ** 30
    return id(a), id(b)


print(f1())  # (140714000246400, 2355781138896)
print(f2())  # (140714000246400, 2355781138896)

但是在Python3.8中，如果是通过 python xxx.py的方式执行的话，即便是大整数、并且不再同一个编译单元的常量池中，它们的地址也是一样的，说明Python在3.8版本的时候做了优化。

另外，如果没有特殊说明，那么我们这个系列的所有代码都是在Python3.8下执行的。说实话，我就是因为发现在Python3.8中，打印的地址都是一样的，才在上面试了一下Python3.6。但是Python3.8中具体是怎么优化的，这里就暂时不讨论了(明明是你没有仔细研究)。

整数运算

整数溢出是程序开发中一大难题，由此引发的 BUG 不计其数，而且相当隐蔽。之前使用golang刷LeetCode的时候，怎么也通不过，最后发现是因为LeetCode后台有一个测试用例比较特殊，导致整数太大，golang中的int64存不下。而Python 选择从语言层面彻底解决这个痛点，殚心竭虑地设计了整数对象。而我们也探索了整数对象，并初步掌握了整数对象的内部结构。

Python中的整数是串联了多个C中的digit(uint32_t)，通过一个C数组的形式来实现整数的表示。这么做的好处就是Python中的整数没有长度限制了，因此不会溢出(而浮点数使用C的double，所以它会溢出)。之所以不会溢出，是因为数组是没有长度限制的，所以只要你的内存足够，就可以算任意大的数。所以Python表示：存不下？会溢出？这都不是事儿，直接继续往数组里面塞digit就ok了。

这里再重温一下PyLongObject的数据结构，我们说它是一个变长对象。ob_size指的是数组的长度，并且它除了表示长度还能体现出整数的正负，而ob_digit这个数组只用来存储其绝对值。

但是说实话，用整数数组实现大整数的思路其实平白无奇，但难点在于大整数 数学运算 的实现，它们才是重点，也是也比较考验编程功底的地方。

所以我们在分析浮点数的时候，一直说整数要比浮点数复杂，原因就在于此。浮点数相加的话直接两个double相加即可，但是整数相加可就没有那么简单了。

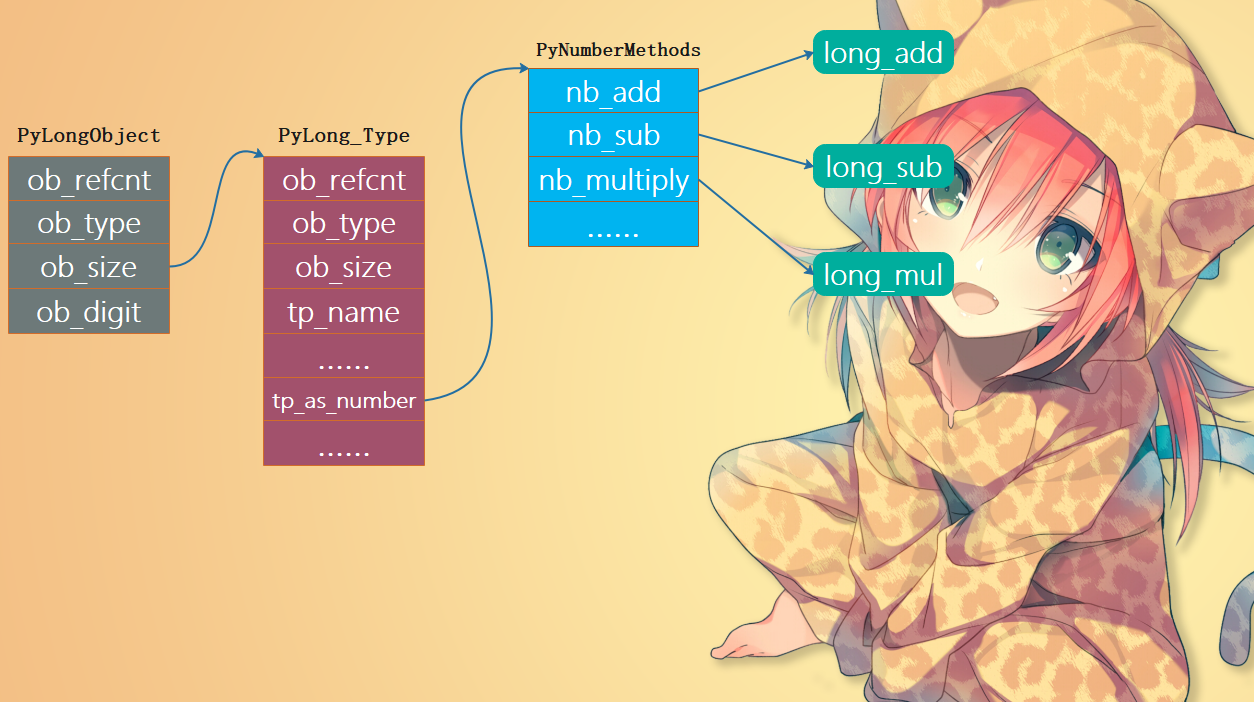
整数支持的操作定义在什么地方相信不用我说了，直接去longobject.c中查看就可以了，根据浮点数的经验我们知道PyLong_Type中的tp_as_number成员也指向了PyNumberMethods结构体实例，里面的成员都是指向与整型运算相关的函数的指针。

注意：图中有一个箭头画错了，应该是 ob_type 指向 PyLong_Type，但图中不小心变成了 ob_size。

整数的大小比较

先来看看Python中的整数在底层是如何比较的吧。

static int
long_compare(PyLongObject *a, PyLongObject *b)
{	
    //sign是一个8字节的long, 用来表示a和b之间的比较结果
    //如果a == b, 那么sign = 0; 如果a > b, 那么sign > 0; 如果a < b, 那么sign < 0
    Py_ssize_t sign;
	
    //Py_SIZE是一个宏:获取对象的ob_size,除此之外我们之前还见到了Py_REFCNT和Py_TYPE, 用来获取对象的引用计数和类型指针
    //如果两个整数的ob_size不一样, 我们说a和b一定不相等, 所以可以直接比较出大小
    if (Py_SIZE(a) != Py_SIZE(b)) {
        //如果一正一负, 那么肯定正的大, 因为ob_size还体现整数的正负, 所以正的ob_size对应的整数也会更大
        //如果都为正, 那么ob_size越大, 对应数组元素就越多, 显然整数就越大
        //如果都为负, 那么ob_size越大, 其绝对值就越小, 因为越接近0,所以对应的整数的绝对值也越小
          //但因为是负数,所以乘上-1之后,所以整数值反而会越大。比如: 1 < 100, 但是乘上-1之后, 小于号就要变成大于号
        //因此无论是哪种情况，如果两个整数的ob_size不一样，是可以直接比较出大小的。
        sign = Py_SIZE(a) - Py_SIZE(b);
        //所以sign > 0的话a > b, sign < 0的话a < b, 因为ob_size不一样, 所以sign不可能等于0
    }
    else {
        //如果相等, 那么说明a和b的符号相同, 数组中使用的digit也是一样的
        //那么接下来就只能挨个比较数组中的digit了
        //这里是获取数组的长度, 赋值给变量i
        Py_ssize_t i = Py_ABS(Py_SIZE(a));
        //我们之前说，一个digit存不下，那么会使用两个digit, 以此类推
        //并且代表整数高位的digit会放在后面, 而比较两个数的大小显然是从高位开始比
        //因此遍历数组是从后往前遍历的, 先比较a -> ob_digit[n]和 b -> ob_digit[n]
        //如果一样就比较a -> ob_digit[n-1]和a -> ob_digit[n-1],直到将数组的元素全部比完,显然只要有一个不一样,就可以直接决定绝对值的大小
        while (--i >= 0 && a->ob_digit[i] == b->ob_digit[i])
            //进行while循环, i是数组的长度, 因此数组的最大索引是i - 1, 所以这里的--i会先将i自减1,再判断自减1之后的i是否>=0
            //然后比较a->ob_digit[i]和b->ob_digit[i], 如果数组内元素全部一样, 那么循环结束之后i肯定是-1,只要有一个不一样, 那么i一定>=0
            ;
        if (i < 0)
            //所以如果i < 0,说明两个整数的数组全部一样, 因此两个整数是一样的
            //所以sign = 0
            sign = 0;
        else {
            //否则的话, 说明数组中索引为i的元素不一样, 那么直接相减就可以了
            //如果sign大于0, 显然a对应的绝对值比大, 否则a对应的绝对值比b小
            sign = (sdigit)a->ob_digit[i] - (sdigit)b->ob_digit[i];
            if (Py_SIZE(a) < 0)
                //但是我们说计算的是绝对值，如果ob_size小于0，绝对值越大其值反而越小，那么sign还要乘上-1
                sign = -sign;
        }
    }
    //因此最终: a > b则sign > 0, a < b则sign < 0, a == b则sign == 0
    //然后这里是一个嵌套的三元表达式, sign大于0则直接返回1表示a > b, 小于0返回-1表示a < b, 等于0则返回0表示a == b
    return sign < 0 ? -1 : sign > 0 ? 1 : 0;
}

所以我们看到Python中的整数就是按照上面这种方式比较的，总的来说就是先比较ob_size，ob_size不一样则可以直接比较。如果ob_size一样的话，那么会从后往前挨个比较数组中的元素，最终确定大小关系。

整数的相加

再来看看Python中的整数在底层是如何相加的，加法的实现显然是long_add，我们看一下。

static PyObject *
long_add(PyLongObject *a, PyLongObject *b)
{	
    //a和b是两个PyLongObject *
    //z显然是指向a和b相加之后的PyLongObject
    PyLongObject *z;
	
    //CHECK_BINOP是一个宏, 接收两个指针, 检测它们是不是都指向PyLongObject
    CHECK_BINOP(a, b);
	
    //判断a和b的ob_size的绝对值是不是都小于等于1, 如果是的话, 那么说明数组中最多只有一个元素
    //数组没有元素,说明整数是0;有一个元素,那么直接取出来、再判断正负号即可,然后直接相加。
    //所以显然这里走的是快分支,因为绝对值超过2 ** 30 - 1的整数还是比较少的
    if (Py_ABS(Py_SIZE(a)) <= 1 && Py_ABS(Py_SIZE(b)) <= 1) {
        //MEDIUM_VALUE是一个宏, 接收一个abs(ob_size) <= 1的PyLongObject的指针
        //如果ob_size是0, 那么结果为0; 如果ob_size绝对值为1, 那么结果为 ob_digit[0] 或者 -ob_digit[0]
        //所以直接将MEDIUM_VALUE(a) + MEDIUM_VALUE(b)之后的结果转成PyLongObject,然后返回其指针即可
        //因此如果数组中元素不超过1个的话, 那么显然是可以直接相加的
        return PyLong_FromLong(MEDIUM_VALUE(a) + MEDIUM_VALUE(b));
    }
    //走到这里, 说明至少有一方的ob_size大于1
    //如果a < 0
    if (Py_SIZE(a) < 0) {
        //如果a < 0并且b < 0
        if (Py_SIZE(b) < 0) {
            //说明两者符号相同, 那么通过x_add直接将两个整数相加即可
            //这个x_add专门用于整数的绝对值相加,并且会返回PyLongObject *,它的实现我们后面会说
            //所以z指向的PyLongObject的内部成员是已经设置好了的
            //只不过x_add加的是两者的绝对值, z指向的PyLongObject内部ob_type的符号我们还需要再度判断一下
            z = x_add(a, b);
            if (z != NULL) {
                assert(Py_REFCNT(z) == 1);
                //因为a和b指向的整数都是负数, 所以将相加之后还要将ob_size乘上-1
                Py_SIZE(z) = -(Py_SIZE(z));
            }
        }
        else
            //走到这里说明a < 0并且b > 0, 那么直接让b - a即可, 此时得到的结果一定是正
            //因此不需要考虑ob_size的符号问题
            z = x_sub(b, a);
    }
    else {
        //走到这里说明a > 0并且b < 0, 所以让a - b即可
        if (Py_SIZE(b) < 0)
            z = x_sub(a, b);
        else
            //此时两个整数均为正, 直接相加
            z = x_add(a, b);
    }
    //返回z的指针
    return (PyObject *)z;
}

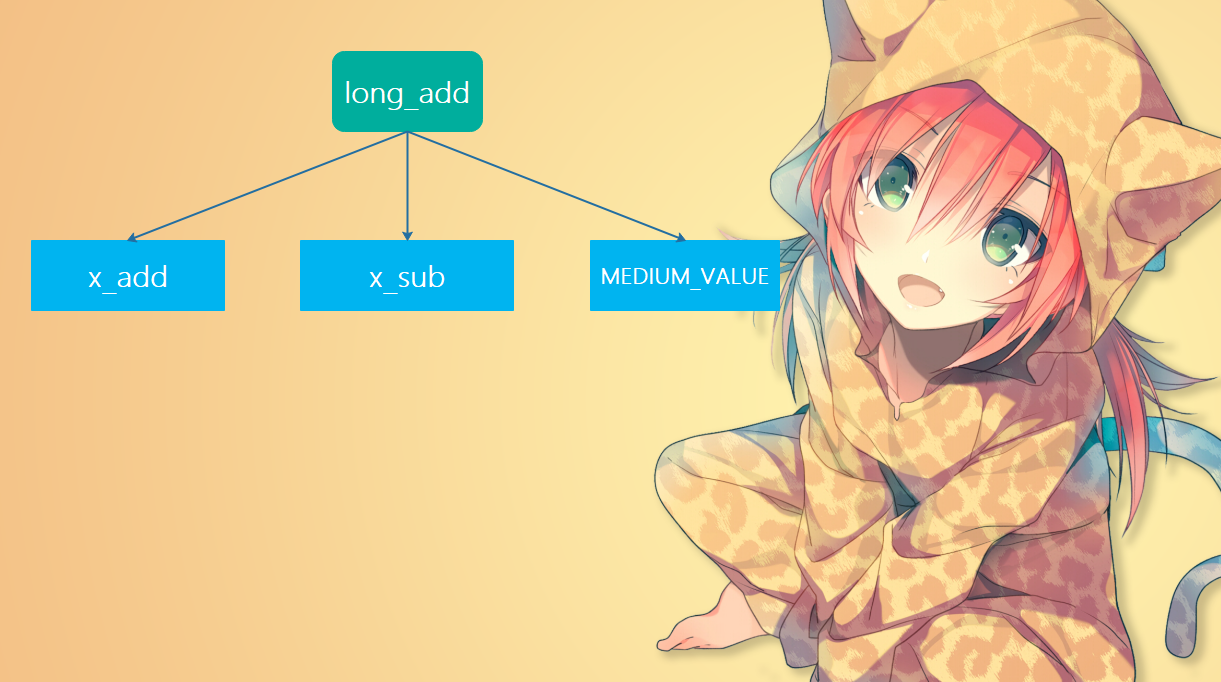
所以long_add这个函数并不长，但是调用了辅助函数x_add和x_sub，显然核心逻辑是在这两个函数里面。至于long_add函数，它的逻辑如下：

• 1. 定义一个变量z, 用于保存计算结果;
• 2. 判断两个整数底层对应的数组是不是都不超过1, 如果是的话那么通过宏MEDIUM_VALUE直接将其转成C中的一个digit, 然后直接相加、返回即可。显然这里走的是快分支,或者快速通道;
• 3. 但如果有一方ob_size绝对值不小于1, 那么判断两者的符号。如果都为负,那么通过x_add计算两者绝对值之和、再将ob_size乘上-1即可;
• 4. 如果a的ob_size小于0, b的ob_size大于0, 那么通过x_sub计算b和a绝对值之差即可;
• 5. 如果a的ob_size大于0, b的ob_size小于0, 那么通过x_sub计算a和b绝对值之差即可;
• 6. 如果a的ob_size大于0, b的ob_size大于0, 那么通过x_add计算让b和a绝对值之和即可;

所以Python中整数的设计非常的巧妙，ob_digit虽然是用来维护具体数值，但是它并没有考虑正负，而是通过ob_size来表示整数的正负号。这样运算的时候，计算的都是整数的绝对值，因此实现起来会方便很多。将绝对值计算出来之后，再通过ob_size来判断正负号。

因此long_add将整数加法转成了 “绝对值加法(x_add)”和”绝对值减法(x_sub)”：

• x_add(a, b), 计算两者的绝对值之和, 即:|a| + |b|;
• x_sub(a, b), 计算两者的绝对值之差, 即:|a| - |b|;

由于绝对值加、减法不用考虑符号对计算结果的影响，实现更为简单，这是Python将整数运算转化成绝对值运算的缘由。虽然我们还没看到x_add和x_sub是如何对整数的绝对值进行相加和相减运算的，但也能从中体会到程序设计中逻辑的 划分 与 组合 的艺术，优秀的代码真的很美。

那么下面我们的重心就在x_add和x_sub中了，看看它们是如何对大整数绝对值进行运算的。但是你可能会有疑问，大整数运算肯定很复杂，效率会差吧。显然这是必然的，整数数值越大，整数对象底层数组越长，运算开销也就越大。好在运算处理函数均以快速通道对小整数运算进行优化，将额外开销降到最低。

比如上面的long_add，如果a和b对应的整数的绝对值都小于等于2 ^ 30 - 1，那么会直接转成C中的整型进行运算，性能损耗极小。并且走快速通道的整数的范围是：-(2 ^ 30 - 1) ~ 2 ^ 30 - 1，即：-1073741823 ~ 1073741823，显然它可以满足我们绝大部分的运算场景。

​ 绝对值加法x_add：

在介绍绝对值加法之前，先来看看几个宏，先不管它们是干什么的，会在x_add中有体现：

//longintrepr.h
#define PyLong_SHIFT    30
#define PyLong_BASE     ((digit)1 << PyLong_SHIFT)
#define PyLong_MASK     ((digit)(PyLong_BASE - 1))
//所以PyLong_MASK等于(1 << 30) - 1, 就等于2 ** 30 - 1, 说明32个位, 前两个位为0, 后面三十个位则都是1

此外，再想象一下我们平时算加法的时候是怎么算的：

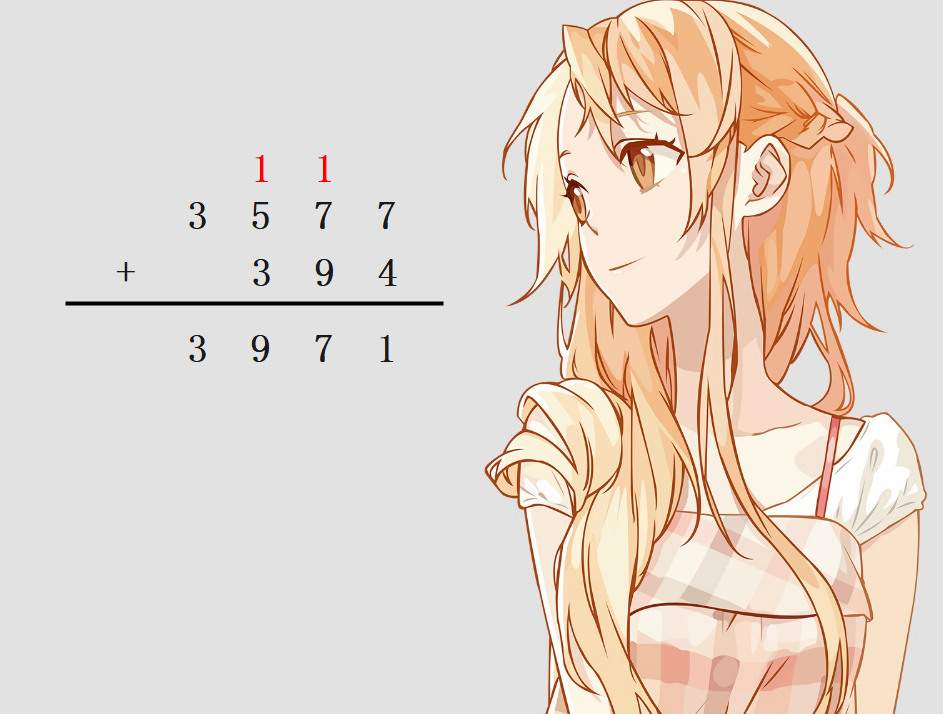
而x_add在逻辑和上面是类似的，下面分析x_add的实现：

static PyLongObject *
x_add(PyLongObject *a, PyLongObject *b)
{	
    //显然a和b指向了两个要想加的整数对象
    //这里获取a和b的ob_size的绝对值
    Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
    //根据a和b的相加结果所创建的新的PyLongObject的指针
    PyLongObject *z;
    //循环变量
    Py_ssize_t i;
    //重点也是最难理解的地方: carry用于每个部分的运算结果(可不是大神带你carry哦)
    digit carry = 0;
	
    //如果size_a小于size_b
    if (size_a < size_b) {
        //那么将a和b进行交换, 以及size_a和size_b也进行交换, 为什么这么做呢?因为方便
        //我们小时候计算两个整数相加时候, 如果一个位数多,一个位数少, 也会习惯将位数多的放在左边
        //最终从右往左, 也就是从低位往高位逐个相加, 大于10则进1
        { PyLongObject *temp = a; a = b; b = temp; }
        { Py_ssize_t size_temp = size_a;
            size_a = size_b;
            size_b = size_temp; }
        //如果size_a和size_b相等, 或者size_a大于size_b, 那么该if就无需执行了
    }
    //这里是创建一个ob_size为size_a + 1的PyLongObject, 然后返回其指针
    z = _PyLong_New(size_a+1);
    //但为什么是size_a + 1呢?
    //因为此时size_a 一定不小于 size_b, 那么a和b相加之后的z的ob_size一定不小于size_a
    //但是也可以也可能比size_a多1, 比如: a = 2 ** 60 - 1, b = 1
    //所以相加之后结果为2 ** 60次方, 所以ob_size就变成了3, 因此在创建z的时候，ob_digit的容量会等于size_a + 1
    
    //正常情况下, z是一个PyLongObject *, 但如果z == NULL, 表示分配失败(解释器也会异常退出)
    //但说实话, 除非你内存不够了, 否则这种情况不会发生
    if (z == NULL)
        return NULL;
    
    //重点来了, 如果a和b的ob_size不一样, 那么size_a会大于size_b
    //所以显然是先以size_b为准, 两者从低位向高位依次对应相加; 当b到头了, 再单独算a的剩余部分;
    //假设size_a == 4, size_b == 2, 对应到ob_digit的话
    //就是a -> ob_digit[0] + b -> ob_digit[0], 作为z -> ob_digit[0], 当然还需要考虑进位, 下面说
    //然后a -> ob_digit[1] + b -> ob_digit[1], 作为z -> ob_digit[1], 此时b到头了
    //继续a -> ob_digit[2]作为z -> ob_digit[2], a -> ob_digit[3]作为z -> ob_digit[3]
    //此时a和b相加就结束了, 如果不考虑相加进位的话, 那么整体流程就是这个样子。然后我们继续往下看
    
    //从索引为0开始遍历, 以i < size_b为条件
    for (i = 0; i < size_b; ++i) {
        //将a->ob_digit[i] + b->ob_digit[i]作为carry, 显然carry如果没有超过2 ** 30 - 1的话
        //显然它就是z -> ob_digit[i]
        carry += a->ob_digit[i] + b->ob_digit[i];
        //但是carry是可能溢出的, 所以z -> ob_digit[i] = carry & PyLong_MASK
        //这个PyLong_MASK就是我们在介绍x_add之前先介绍的几个宏之一, 它表示的是2 ** 30 - 1
        //我们说它的前两个位为0, 后面三十个位全是1, 因此对于后面三十个位来说, 在和carry进行"与运算"之后,对应的位还和carry保持一致
        //所以在carry小于等于2 ** 30 - 1的时候carry & PyLong_MASK就等于carry
        //但如果carry大于2 ** 30 - 1, 由于PyLong_MASK的前两位为0, 所以这一步可以确保carry不会超过2 ** 30 - 1
        z->ob_digit[i] = carry & PyLong_MASK;
        //但是carry的前两位显然不可以丢, 所以它们要作用在数组中下一个元素相加的结果上
        //比如a -> ob_digit[0] + b -> ob_digit[0]得到结果正好是2 ** 32 - 1, 那么carry的前两位也是1
        //而数组中下一元素相加之后, 其结果对应的位要比本次循环高出30
        //所以这里将carry右移30位, 然后作用到下一次循环中
        carry >>= PyLong_SHIFT;
    }
    for (; i < size_a; ++i) {
        //如果当b到头了, 那么继续从当前的i开始, 直到i == size_a, 逻辑还是和上面一样的
        //只不过将a->ob_digit[i] + b->ob_digit[i]换成了a->ob_digit[i], 因为b到头了
        carry += a->ob_digit[i];
        //这里也要"与上"PyLong_MASK, 因为也可能存在进位的情况, 拿生活中的99999 + 1为例
        //此时a = 99999, b = 1, 显然第一次循环b就到头了, 但后面单独循环a的时候, 依旧是要加进位的
        //所以这里也是同理
        z->ob_digit[i] = carry & PyLong_MASK;
        //carry右移30位
        carry >>= PyLong_SHIFT;
    }
    //两个循环结束之后, 其实还差一步, 还拿99999 + 1举例子, 按照顺序相加最后得到的是00000
    //因为最后还进了一个1, 所以这里的carry也是同理, 因此z的ob_size要比size_a多1, 目的就在于此
    z->ob_digit[i] = carry;
    //但如果最后的carry没有进位的话, 显然其结果就是0, 所以最后没有直接返回z, 而是返回了long_normalize(z)
    //这个long_normalize函数作用就是从后往前依次检查ob_digit的元素, 如果为0, 那么就将其ob_size减去1, 直到出现一个不为0的元素
    //当然对于我们当前来说, 显然最多只会检查一次
    return long_normalize(z);
}

Python中的整数在底层实现的很巧妙，不理解的话可以多看几遍，然后我们在Python的层面上再反推一下，进一步感受底层运算的过程。

# 假设有a和b两个整数, 当然这里是使用列表直接模拟的底层数组ob_digit
a = [1073741744, 999, 765, 123341]
b = [841, 1073741633, 2332]
# 然后创建z, 表示a和b的相加结果
z = []

# 为了更直观, 我们一步步手动相加
# 首先是将a[0] + b[0], 得到carry
carry = a[0] + b[0]
# 然后carry & (2 ** 30 - 1), 我们看到结果是761
print(carry & (2 ** 30 - 1))  # 761
# 因为如果carry小于等于 2 ** 30 - 1, 那么结果就是carry, 而这里是761, 显然carry肯定大于 2 ** 30 - 1
print(carry > 2 ** 30 - 1)  # True
# 因为carry & (2 ** 30 - 1) == 761, 所以z的第一个元素就是761
z.append(761)


# 然后计算a[1] + b[1]得到新的carry, 但是之前的carry大于 2 ** 30 - 1
# 所以还要再加上之前的右移30位的carry
carry = (carry >> 30) + a[1] + b[1]
# 然后carry & (2 ** 30 - 1)得到809
print(carry & (2 ** 30 - 1))  # 809
# 说明carry依旧大于 2 ** 30 - 1
print(carry > 2 ** 30 - 1)  # True
# 然后z的第二个元素就是809
z.append(809)


# 计算a[2] + b[2]的时候也是同理
carry = (carry >> 30) + a[2] + b[2]
# 但是显然此时的carry已经不大于 2 ** 30 - 1了
print(carry > 2 ** 30 - 1)  # False
# 所以carry和carry & (2 ** 30 - 1)的结果都是carry本身
print(carry, carry & (2 ** 30 - 1))  # 3098 3098
# 说明z的第三个元素是3098
z.append(3098)

# 此时b到头了, 所以直接将a[3]作为carry, 当然我们不知道carry是否大于2 ** 30 - 1
# 所以还是右移30位即可, 不过carry不大于2 ** 30 - 1的话, 那么 carry >> 30 就是0罢了
carry = (carry >> 30) + a[3]
print(carry)  # 123341
# 说明z的最后一个元素是123341, 当然理论上我们还要在对carry和 2 ** 30 - 1进行一次判断
# 当然由于我们知道carry肯定不会超过2 ** 30 - 1, 所以就不判断了
z.append(123341)

# 此时z为[761, 809, 3098, 123341]
print(z)  # [761, 809, 3098, 123341]

# 所以ob_digit为[1073741744, 999, 765, 123341]和[841, 1073741633, 2332]的两个PyLongObject相加
# 得到的新的PyLongObject的ob_digit为[761, 809, 3098, 123341]

# 我们根据ob_digit按照规则转成整数, 那么a + b的结果要和z是相等的
a = 1073741744 + 999 * 2 ** 30 + 765 * 2 ** 60 + 123341 * 2 ** 90
b = 841 + 1073741633 * 2 ** 30 + 2332 * 2 ** 60
z = 761 + 809 * 2 ** 30 + 3098 * 2 ** 60 + 123341 * 2 ** 90
print(a)  # 152688762386380073438430860672944
print(b)  # 2689765870042689307465
print(z)  # 152688762389069839308473549980409

# 显然结果为True, 由此证明我们之前的结论是成立的。
print(a + b == z)  # True

​ 看完绝对值加法x_add之后，再来看看绝对值减法x_sub，显然有了加法的经验之后再看减法会简单很多。

static PyLongObject *
x_sub(PyLongObject *a, PyLongObject *b)
{	
    //依旧是获取两者的ob_size的绝对值
    Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
    //z指向相加之后的PyLongObject
    PyLongObject *z;
    //循环变量
    Py_ssize_t i;
    //如果size_a 小于 size_b, 那么sign就是-1, 否则就是1
    int sign = 1;
    //之前carry保存的相加的结果, borrow保存相减的结果
    //名字很形象, 相加要进位叫carry、相减要结尾叫borrow
    digit borrow = 0;

    //如果size_a比size_b小, 说明a的绝对值比b小
    if (size_a < size_b) {
        //那么令sign = -1, 相减之后再乘上sign
        //因为计算的是绝对值之差, 符号是在绝对值之差计算完毕之后通过sign判断的
        sign = -1;
        //然后依旧交换两者的位置, 相减的时候也确保大的一方在左边
        //相加的时候其实大的一方在左边还是在右边没有太大影响, 但是相减的时候大的一方在左边显然会省事很多
        //但是交换之后再相减, 肯定要变符号, 因此将sign设置为-1
        { PyLongObject *temp = a; a = b; b = temp; }
        { Py_ssize_t size_temp = size_a;
            size_a = size_b;
            size_b = size_temp; }
        //可能有人会有疑问了，那如果a的ob_size是1, b的ob_size是-3，一正一负,此时起到的效果是相加才对啊
        //是的, 所以此时会将a和b传到x_add里面，而不是这里, 后面我们会总结
        //由于ob_digit里面的元素都为正, 所以x_add计算的是绝对值之和，x_sub计算的绝对值之差, 总之在理解逻辑的时候把a和b都想象成正数即可
    }
    else if (size_a == size_b) {
        //这一个条件语句可能有人会觉得费解，我们分析一下
        //如果两者相等, 那么两个ob_digit里面对应的元素也是有几率都相等的
        i = size_a;
        //所以从ob_digit的尾巴开始遍历
        while (--i >= 0 && a->ob_digit[i] == b->ob_digit[i])
            ;
        //如果都相等, 那么i会等于-1
        if (i < 0)
            //所以直接返回0即可
            return (PyLongObject *)PyLong_FromLong(0);
        //下面下面是为了计算相减之后的PyLongObject的ob_size
        //如果对应元素不相等, 假设a的ob_digit里面的元素是[2, 3, 4, 5], b的ob_digit是[1, 2, 3, 5]
        //因此上面的while循环结束之后, i会等于2, 显然只需要计算[2, 3, 4]和[1, 2, 3]之间的差即可, 因为最高位的5是一样的
        //然后判断索引为i时, 对应的值谁大谁小
        if (a->ob_digit[i] < b->ob_digit[i]) {
            //如果a->ob_digit[i] < b->ob_digit[i], 那么同样说明a小于b, 因此将sign设置为-1, 然后交换a和b的位置
            sign = -1;
            { PyLongObject *temp = a; a = b; b = temp; }
        }
        //因为做减法, 所以size_a和size_b直接设置成i + 1即可, 因为高位在减法的时候会被抵消掉, 所以它们完全可以忽略
        size_a = size_b = i+1;
    }
    //这里依旧是申请空间
    z = _PyLong_New(size_a);
    //申请失败返回NULL
    if (z == NULL)
        return NULL;
    
    //然后下面的逻辑和x_add是类似的
    for (i = 0; i < size_b; ++i) {
        //让a->ob_digit[i] - b->ob_digit[i], 但如果存在借位, 那么还要减掉
        //但是问题来了, 我们说digit貌似是无符号的吧, 但是对于低位来说a->ob_digit[i] 是完全可以小于 b->ob_digit[i]的
        //但是这样减出来不成负数了, 所以C语言中有这么个特点, 比如：这里相减得到的是-100
        //那么结果就是2 ** 32 - 100, 因为digit是无符号32位, 所以存储的负数会变成 2 ** 32 + 该负数, 或者2 ** 32 - 负数的绝对值
        //以我们平时做的减法为例：32 - 19, 我们知道结果是13, 但是低位的2减去低位的9结果是-7, 如果是负数
        //那么要像高位借个1, 从而得到10,因此最后一位是10 - 7 = 3
        //以此为例, a -> ob_digit[i] - b -> ob_digit[i], 如果小于0, 那么肯定要像数组中i + 1的元素进行借位, 但我们说它会比当前高30个位
        borrow = a->ob_digit[i] - b->ob_digit[i] - borrow;
        //因此这里借个1, 借的就不是10了, 而是2 ** 30次方
        //所以borrow为负, 那么结果显然加上2 ** 30才对, 但是当前borrow加的是2 ** 32次方
        //所以将borrow 还要 与上 PyLong_MASK，然后其结果才是z->ob_digit[i]的值
        z->ob_digit[i] = borrow & PyLong_MASK;
        //如果真的借了个1, 那么ob_digit中下一个元素肯定是要减去1的, 所以borrow右移30位
        borrow >>= PyLong_SHIFT;
        //和1进行与运算, 如果a -> ob_digit[i] - b -> ob_digit[i]为负, 那么就必须要借位
        //但由于digit只用30个位, 因此再加上2 ** 32次方之后，其结果的第31位一定是1
        //所以borrow右移30位之后, 再和1进行与运算之后结果肯定是1, 由此可以判断这次相减一定是借位了
        //如果为0代表结果为正、没有加上2 ** 32次方,那么结果borrow & 1的结果就是0
        borrow &= 1; 
        //所以Python底层的整数只用了30个位真的非常巧妙, 尤其是在减法的时候
        //因为借位一次借2 ** 30, 可由于C的特性会加上2 ** 32次方, 但是它们的结果只有前两个高位不一样, 后面30个位是一样的
        //所以再与上PyLong_MASK, 所以就等价于加上了2 ** 30次方，从而得到正确的结果
        //但如果一旦借位, 那么数组下一个元素要减去1。但问题是怎么判断它有没有借位呢？判断有没有借位就是判断两个元素相减之后是否为负
        //如果为负数,那么C会将这个负数加上2 ** 32次方, 而两个不超过2 ** 30 - 1的数相减得到的负数的绝对值显然也不会超过2 ** 30 - 1
        //换句话说其结果对应的第31位一定是0, 那么再和32个位全部是1的2 ** 32次方相加, 得到的结果的第31位一定是1
        //所以再让borrow右移30位、并和1进行与运算。如果结果为1, 证明相减为负数, 确实像下一个元素借了1, 因此下一次循环的会减去1
        //如果borrow为0, 那么就证明a->ob_digit[i] - b->ob_digit[i]得到的结果为正,根本不需要借位, 所以下一次循环等于减了一个0
    }
    
    //如果size_a和size_b一样, 那么这里的for循环是不会满足条件的, 但不一样的话, 肯定会走这里
    for (; i < size_a; ++i) {
        //我们看到这里的逻辑和之前分析x_add是类似的
        borrow = a->ob_digit[i] - borrow;
        z->ob_digit[i] = borrow & PyLong_MASK;
        borrow >>= PyLong_SHIFT;
        borrow &= 1; 
    }
    //只不过由于不会产生进位, 因此不需要对borrow再做额外判断, x_add中最后还要判断carry有没有进位
    assert(borrow == 0);
    if (sign < 0) {
        //如果sign < 0, 那么证明是负数
        Py_SIZE(z) = -Py_SIZE(z);
    }
    //最后同样从后往前将z -> ob_digit中为0的元素删掉, 直到遇见一个不为0的元素, 比如: 10000 - 9999, 虽然位数多, 但是结果是1
    //而z -> ob_digit在申请空间的时候只是根据长度申请的, 所以最后还需要这样的一次判断
    return long_normalize(z);
}

所以Python整数在底层的设计确实很精妙，尤其是在减法的时候，强烈建议多看几遍回味一下。

整数的相减

整数的相减调用的是long_sub函数，显然long_sub和long_add的思路都是一样的，核心还是在x_add和x_sub上面，所以long_sub就没有什么可细说的了。

static PyObject *
long_sub(PyLongObject *a, PyLongObject *b)
{	
    //z指向a和b相加之后的PyLongObject
    PyLongObject *z;
    //判断a和b是否均指向PyLongObject
    CHECK_BINOP(a, b);
	
    //这里依旧是快分支
    if (Py_ABS(Py_SIZE(a)) <= 1 && Py_ABS(Py_SIZE(b)) <= 1) {
        //直接相减，然后转成PyLongObject返回其指针
        return PyLong_FromLong(MEDIUM_VALUE(a) - MEDIUM_VALUE(b));
    }
    //a小于0
    if (Py_SIZE(a) < 0) {
        //a小于0，b小于0
        if (Py_SIZE(b) < 0)
            //调用绝对值减法, 因为两者符号一样
            z = x_sub(a, b);
        else
            //此时两者符号不一样，那么相加起到的是相加的效果
            z = x_add(a, b);
        if (z != NULL) {
            //但是x_add和x_sub运算的是绝对值, x_sub中考虑的sign是基于绝对值而言的
            //比如：x_sub接收的a和b的ob_size分别是-5和-3, 那么得到的结果肯定是正的, 因为会用绝对值大的减去绝对值小的
            //而显然这里的结果应该是负数, 所以还要乘上-1
            
            //如果x_sub接收的a和b的ob_size分别是-3和-5, 由于还是用绝对值大的减去绝对值小的,所以会交换、从而变号，得到的结果是负的
            //而显然这里的结果应该是正数, 所以也要乘上-1
            
            //至于x_add就更不用说了, 当a为负、b为正的时候, a - b，就等于a和b的绝对值相加乘上-1
            assert(Py_SIZE(z) == 0 || Py_REFCNT(z) == 1);
            Py_SIZE(z) = -(Py_SIZE(z));
        }
    }
    else {
        //a大于0, b小于0, 所以a - b等于a和b的绝对值相加
        if (Py_SIZE(b) < 0)
            z = x_add(a, b);
        else
            //a大于0, b大于0, 所以直接绝对值相减即可
            //而正数等于其绝对值, 所以x_sub里面考虑的符号就是真正的结果的符号
            //如果是上面的负数, 那么还要乘上-1
            z = x_sub(a, b);
    }
    //返回结果
    return (PyObject *)z;
}

所以关于什么时候调用x_add、什么时候调用x_sub，我们总结一下，总之核心就在于它们都是对绝对值进行运算的，掌握好这一点就不难了：

a + b

• 如果a是正、b是正，调用x_add(a, b)，直接对绝对值相加返回结果
• 如果a是负、b是负，调用x_add(a, b)，但相加的是绝对值，所以long_add中在接收到结果之后还要对ob_size乘上-1
• 如果a是正、b是负，调用x_sub(a, b)，此时等价于a的绝对值减去b的绝对值。并且x_sub是使用绝对值大的减去绝对值小的，如果a的绝对值大，那么显然正常；如果a的绝对值小，x_sub中会交换，但同时也会自动变号，因此结果也是正常的。举个普通减法的例子：5 + -3, 那么在x_sub中就是5 - 3; 如果是3 + -5, 那么在x_sub中就是-(5 - 3), 因为发生了交换。但不管那种情况，符号都是一样的
• 如果a是负、b是正，调用x_sub(b, a)，此时等价于b的绝对值减去a的绝对值。所以这个和上面a是正、b是负是等价的。

所以符号相同，会调用x_add、符号不同会调用x_sub。

a - b

• 如果a是正、b是负，调用x_add(a, b)直接对a和b的绝对值相加即可
• 如果a是正、b是正，调用x_sub(a, b)直接对a和b的绝对值相减即可，会根据绝对值自动处理符号，而a、b为正，所以针对绝对值处理的符号，也是a - b的符号
• 如果a是负、b是正，调用x_add(a, b)对绝对值进行相加, 但是结果显然为负，因此在long_sub中还要对结果的ob_size成员乘上-1
• 如果a是负、b是负，调用x_sub(a, b)对绝对值进行相减, 会根据绝对值自动处理符号, 但是在为负的情况下绝对值越大，其值反而越小, 因此针对绝对值处理的符号，和a - b的符号是相反的。所以最终在long_sub中，也要对结果的ob_size成员乘上-1。举个普通减法的例子：-5 - -3, 那么在x_sub中就类似于5 - 3; 如果是-3 - -5, 那么在x_sub中就类似于-(5 - 3), 因为发生了交换。但不管那种情况得到的值的正负号都是相反的，所以要再乘上-1

所以符号相同，会调用x_sub、符号不同会调用x_add。

​ 所以可以仔细回味一下Python中整数的设计思想，以及运算方式。为什么只使用digit的30个位, 以及在相加、相减的时候是怎么做的。

​ 当然还有乘法和除法，乘法Python内部采用的是效率更高的karatsuba算法，相当来说比较复杂，有兴趣可以自己查看一下。重点还是了解Python中的整数在底层是怎么存储的，以及为什么要这么存储。

小结

这一节我们介绍了整数的底层实现，并分析了Python中的整数为什么不会溢出，以及Python如何计算一个整数所占的字节。当然我们还说了小整数对象池，以及通过分析源码中的long_add和long_sub来了解底层是如何对整数进行运算的。