Detecting Logic Bugs in Graph Database Management Systems via Injective and Surjective Graph Query Transformation
Detecting Logic Bugs in Graph Database Management Systems via Injective and Surjective Graph Query Transformation
开源代码: https://github.com/YuanchengJiang/GraphGenie
Basic Information:
- Title: Detecting Logic Bugs in Graph Database Management Systems via Injective and Surjective Graph Query Transformation (通过单射和满射图查询转换检测图数据库管理系统中的逻辑错误)
- Authors: Yuancheng Jiang, Jiahao Liu, Jinsheng Ba, Roland H.C. Yap, Zhenkai Liang, and Manuel Rigger
- Affiliation: National University of Singapore (新加坡国立大学)
- Keywords: Graph Databases, Logic Bugs, Metamorphic Testing
- URLs: Paper, GitHub
论文简要 :
- 通过单射和满射图查询转换,该研究提出了一种检测图数据库管理系统中逻辑错误的方法,通过生成变异查询来验证其结果与原始查询的预期关系,从而发现了25个未知的错误,包括16个逻辑错误、3个内部错误和6个性能问题。
背景信息:
- 论文背景: 图数据库管理系统(GDBMSs)是用于存储和查询图数据的系统,但是它们容易受到逻辑错误的影响,导致计算出错误的结果,进而影响依赖于它们的应用程序。
- 过去方案: 过去的方法主要是基于差异测试和变异测试,但是在图查询中存在一些困难,如建立有效的测试预期和生成变异查询。
- 论文的Motivation: 为了解决图数据库管理系统中逻辑错误的检测问题,本研究提出了一种基于图查询转换的方法,通过生成变异查询并验证其结果与原始查询的预期关系,从而有效地检测逻辑错误。
方法:
- a. 理论背景:
- 本文提出了一种称为注射和满射图查询转换(GQT)的方法,用于检测图数据库管理系统(GDBMS)中的逻辑错误。该方法涉及从基本查询派生出一个突变查询,然后比较两个查询的结果以检测GDBMS中的逻辑错误。关键的洞察力在于图查询中的图模式使得可以从基本查询和突变查询之间的注射和满射映射导出系统化的查询转换。
- b. 技术路线:
- 本文实现了注射和满射图查询转换(GQT)作为一个名为GraphGenie的工具,并在6个流行且成熟的GDBMS上进行了评估。使用GraphGenie,他们发现了25个未知的错误,包括16个逻辑错误,3个内部错误和6个性能问题。这证明了GraphGenie在检测GDBMS中的逻辑错误方面的实用性和有效性,有潜力提高依赖于这些GDBMS的应用程序的可靠性。
结果:
- a. 详细的实验设置:
- 本文将注射和满射图查询转换(GQT)作为GraphGenie工具实现,并在6个流行且成熟的GDBMS上进行了评估。评估持续了三个月,并在一台个人电脑上进行了实验,该电脑具有特定的硬件和软件规格,包括Intel(R) Core(TM) i7-9700 CPU @ 3.00GHz,16GB RAM和Ubuntu 20.04.2 LTS作为操作系统。
- b. 详细的实验结果:
- GraphGenie成功地在成熟的GDBMS中发现了25个以前未知的错误,包括16个逻辑错误,3个内部错误和6个性能问题。与两种最先进的方法进行比较,GraphGenie没有产生虚警,而另一种比较的工具产生了虚警。此外,GraphGenie还发现了另一种工具无法发现的6个逻辑错误。作者认为这些结果是令人鼓舞的,并且表明GraphGenie可能成为测试GDBMS的实用工具。
Abstract:
这项工作提出了一种用于检测图数据库管理系统(GDBMSs)中逻辑错误的方法,称为注入式和满射式图查询转换(GQT)。通过对给定查询𝑄进行变异,生成一个新的查询𝑄′,这两个查询的结果集要么语义等价,要么基于变异是彼此的子集或超集。如果结果之间预期的关系不成立,则表明GDBMS中存在逻辑错误。这种方法的关键洞察是,图查询中的图模式允许基于𝑄和𝑄′之间有向边集的注入式和满射式映射来系统地进行查询转换。研究者们实现了这一方法,并将其命名为GraphGenie工具,用于评估6个流行且成熟的GDBMSs。GraphGenie成功发现了25个未知错误,包括16个逻辑错误、3个内部错误和6个性能问题。这些结果证明了GraphGenie在检测GDBMSs中的逻辑错误方面的实用性和有效性,这对于提高依赖这些GDBMSs的应用程序的可靠性具有潜在价值。
Introduction:
背景:
图数据库管理系统(GDBMSs)专为存储和查询图形数据而设计,近年来迅速获得了广泛的流行,并在各个领域中变得越来越普遍。GDBMSs通过操作顶点和边来支持图形数据的存储和匹配,这大大提高了社交网络、推荐系统和程序分析等多种应用的可用性和效率。根据市场统计数据,2023年全球图数据库市场的价值为29亿美元,预计到2028年将增长到73亿美元,复合年增长率为20.2%。这一增长趋势主要由在线模式环境的需求增加和实时大数据挖掘的需求推动。
Logical bugs in graph db and a Motivation Example:
图数据库管理系统(GDBMSs)是复杂的软件系统,使用复杂的算法,因此容易受到逻辑错误的影响,这会导致对给定查询产生错误的结果。与崩溃错误不同,GDBMS中的逻辑错误可能会悄无声息地计算出错误的结果,这通常既不被用户也不被开发者注意到,从而使得修复这类错误变得困难。例如,AgensGraph GDBMS就存在一个逻辑错误,当计算具有循环路径的节点数量时(例如,match (n)-[]-(n) return count(n)),会产生错误的结果。这个错误是由之前一个旨在移除不必要连接的补丁引入的,但该补丁忘记了考虑自连接的情况。
Related work and challenges:
一种方法是使用差异测试[27,55]来比较来自不同gdbms的结果,结果中的任何差异都表明存在潜在的错误。即使基本查询在不同GDBMS(如Neo4j和MemGraph)中也可能产生不同结果,这些差异可能是由于设计上的不一致性,导致误报。
[27] Wei Lin, Ziyue Hua, Luyao Ren, Zongyang Li, Lu Zhang, and Tao Xie. 2022. GDsmith: Detecting Bugs in Graph Database Engines. arXiv preprint arXiv:2206.08530(2022).
[55] Yingying Zheng, Wensheng Dou, Yicheng Wang, Zheng Qin, Lei Tang, Yu Gao,Dong Wang, Wei Wang, and Jun Wei. 2022. Finding bugs in Gremlin-based graph database systems via Randomized differential testing. In Proceedings of the 31st ACM SIGSOFT International Symposium on Software Testing and Analysis 302–313.
另一种方法是利用蜕变测试来生成突变的图查询,并验证它们的结果是否符合先前的期望。在图数据库中,唯一现有的工作[22]是基于谓词划分[42],它旨在通过三元逻辑划分[43]生成三个不相交的子集查询。
[22] Matteo Kamm. 2022. Testing Graph Databases using Predicate Partitioning. Master’s thesis. ETH Zurich.
Approach:
在这项工作中,我们提出了一种新的测试方法,称为注入式和满射式图查询转换(GQT),以有效地检测GDBMS中的逻辑错误。我们方法的核心思想是利用图查询中的图模式(G-Pattern),通过基于有向边集的注入式和满射式映射,系统地生成后续查询。这些后续查询旨在计算与初始查询结果以特定方式相关的结果,任何差异都表明存在逻辑错误。我们的方法考虑了两类有向边集的G-Pattern映射:(1)双射映射和(2)仅注入式或仅满射式映射。
- 使用双射边映射,我们基于查询𝑄生成一个后续查询𝑄′,使得𝑄′的结果集与𝑄的结果集相等(𝑅𝑆(𝑄′)=𝑅𝑆(𝑄))。为了导出后续查询𝑄′,我们引入了一个操作符=○,该操作符随机应用一个查询等价转换。
- 同样地,使用仅注入式或仅满射式边映射,我们基于查询𝑄生成一个后续查询𝑄′,使得𝑄′的结果集要么是𝑄的结果集的超集(𝑅𝑆(𝑄′)⊇𝑅𝑆(𝑄)),要么是子集(𝑅𝑆(𝑄′)⊆𝑅𝑆(𝑄)),这意味着后续查询的结果集比基础查询的结果集大或小(至少相等)。为了导出这种比较关系,我们引入了变异操作符>○和<○,这些操作符随机应用一个查询泛化或限制转换。
我们的方法基于注入式和满射式有向边映射创建图查询转换,涉及三个操作符(即=○, >○, 和<○),我们使用这些操作符从基础查询生成测试用例。
An motivation example:
在这个例子中,使用图查询转换(GQT)方法在RedisGraph中发现了一个逻辑错误。测试案例包括一个基础查询𝑄和一个通过变异图模式构造的等价查询𝑄=○。在变异的查询中,图模式的顺序被反向表示,同时保持有向边集之间的双射映射,这允许生成一个应该与原始查询给出相同结果的替代查询。然而,这对语义上等价的查询意外地输出了不一致的结果,因此确定RedisGraph存在逻辑错误。该错误后来被开发者确认并修复。

这条语句是使用Cypher查询语言编写的,Cypher是Neo4j图数据库的查询语言,但也被其他图数据库系统采用或支持。这条具体的查询语句的目的是在图数据库中执行一个特定的图模式匹配。
MATCH (s1:B)-[*1..2]-(s3:A):这部分是一个图模式匹配表达式。MATCH是Cypher中用于指定图模式匹配的关键字。这个表达式寻找图中的两个节点s1和s3,其中s1标记为B类型,s3标记为A类型。-[*1..2]-表示s1和s3之间的路径,可以是直接相连的(即边的数量为1),或者通过一个中间节点相连(即边的数量为2)。这个路径不分方向,意味着s1到s3或s3到s1的路径都是有效的。RETURN count(s1);:这部分指定了查询的返回值。RETURN是Cypher中用于指定返回什么数据的关键字。count(s1)是一个聚合函数,用于计算满足匹配条件的s1节点的数量。在图数据库中查找所有标记为
B的节点s1,这些节点通过一条长度为1到2的路径与标记为A的节点s3相连,然后返回这样的s1节点的总数。
Evaluation and Contributions:
在这项工作中,研究团队开发了一个名为GraphGenie的工具,以评估他们提出的注入式和满射式图查询转换(GQT)技术的有效性。GraphGenie支持两种流行的图查询语言:Cypher和Gremlin,并在六个成熟的图数据库管理系统(GDBMS)上进行了测试,包括Neo4j、RedisGraph、AgensGraph、TinkerPop、JanusGraph和HugeGraph。通过这些测试,研究团队发现了总共25个之前未知的错误,包括16个逻辑错误(其中6个已修复,3个已确认)、3个内部错误(全部已修复)和6个性能问题(全部收到了积极反馈)。
此外,研究团队将GraphGenie与两种基于差异测试和查询分割的最新技术进行了比较,这两种技术分别由工具Grand和GDBMeter实现。与Grand相比,GraphGenie没有产生任何误报(Grand的误报率超过80%)。与GDBMeter相比,GraphGenie能够识别出GDBMeter未能发现的6个逻辑错误。这些结果表明GraphGenie是一个有前景的GDBMS测试工具。
总结其贡献,可以归纳为以下几点:
- 提出了一种新颖有效的方法:注入式和满射式图查询转换(GQT),这是一种用于识别GDBMS中逻辑错误的新方法。该方法通过在常见查询元素上创建可扩展的图转换,基于有向边映射生成后续查询,并使用三个操作符(即=○, >○, <○)创建测试神谕来揭示逻辑错误。
- 开发了一个实用工具GraphGenie:基于上述方法,GraphGenie能够生成有效的基础查询,结合规则生成变异查询,并且能够在没有任何误报的情况下识别逻辑错误。该工具支持两种主要的图查询语言。
- 在成熟的GDBMS中发现了多种逻辑错误:GraphGenie发现了包括16个逻辑错误、几个内部错误和严重性能问题在内的总共25个之前未知的错误。GraphGenie提交的错误报告得到了开发者的积极接收和认可。
Background:
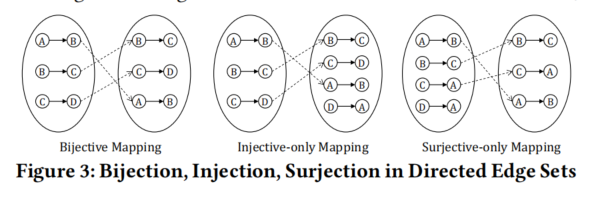
本文的背景部分提供了对图数据库管理系统(GDBMSs)、图查询语言以及映射类型(注入、满射和双射)的基础介绍,这些都是理解和评估GDBMSs中逻辑错误检测方法的关键概念。
图数据库管理系统(GDBMSs)
- GDBMSs使用各种图模型来表示数据,本文特别关注标签属性图模型,这是在如Neo4j、RedisGraph和TinkerPop等先进GDBMS中最广泛使用的模型。
- 这些系统大而复杂,例如,Neo4j最新版本的代码行数超过一百万行。
图查询语言
- 图查询语言(如Cypher和Gremlin)用于与GDBMSs交互。本文主要以Cypher查询语言来阐述方法。
- Cypher查询包含几个元素:匹配(Match)指定需要匹配的图模式;图模式(G-Pattern)指定节点和边的匹配模式;谓词(Predicate)指定匹配查询边的过滤条件;返回(Return)指定结果,可以包括聚合函数如count();其他(Others)指定结果集的额外约束,如排序(order by)、限制(limit)和跳过(skip)。
- 节点和边通过连字符(-)和箭头(> 或 <)连接,表示边的方向。Cypher还允许表示变长的复杂图模式(如[*1..2]表示边长从1到2的图模式)。
注入、满射和双射
- 注入(Injection)、满射(Surjection)和双射(Bijection)描述了函数如何将其域(函数参数)映射到陪域(函数结果)。
- 注入表示一对一映射,即陪域中的每个元素最多由域中的一个元素映射。
- 满射表示“到上”的映射,如果陪域中的每个元素至少由域中的一个元素映射。
- 双射是同时具有注入性和满射性的函数。
注入(Injection)- 一对一映射
假设我们有两个集合:A = {1, 2, 3} 和 B = {a, b, c, d}。一个函数f从A到B是注入的,如果A中的每个元素都映射到B中的一个唯一元素,而且不同的元素映射到不同的元素。
- f(1) = a
- f(2) = b
- f(3) = c
在图数据库中,注入映射可以用来描述一个场景,其中每个查询模式(或子图模式)在目标图中找到的匹配是唯一的。例如,考虑一个社交网络图,节点代表人,边代表人与人之间的朋友关系。如果我们执行一个查询来找到具有特定属性的人(比如,名字为”John”),并且在图中只有一个”John”,那么这个查询就可以被视为是注入的,因为我们查询的每个实例(在这个例子中只有一个)都映射到图中的一个唯一节点。
满射(Surjection)- 到上映射
继续使用集合A = {1, 2, 3} 和 B = {a, b, c}。一个函数f从A到B是满射的,如果B中的每个元素至少由A中的一个元素映射。
- f(1) = a
- f(2) = b
- f(3) = b
满射在图数据库中可以用来描述一个查询,它能够覆盖图中的所有目标节点或边。例如,如果我们的查询是找到图中所有的人节点,不管它们的属性如何,只要每个人节点至少被查询匹配一次,这个查询就是满射的。在实际应用中,满射可能不那么常见,因为大多数查询都是为了找到满足特定条件的一部分节点或边,而不是全部。
双射(Bijection)- 一一对应映射
如果集合A = {1, 2, 3} 和集合B = {a, b, c},一个函数f从A到B是双射的,如果它既是注入也是满射。这意味着A中的每个元素都唯一地映射到B中的一个元素,反之亦然。
- f(1) = a
- f(2) = b
- f(3) = c
例如,如果我们有一个图,其中包含特定类型的节点,比如所有的”人”节点都有一个唯一的ID作为属性,那么一个查询,它根据ID查找这些”人”节点,将形成一个双射,因为每个ID都唯一对应一个节点,每个节点也都有一个唯一的ID。
Graph Pattern Mapping
本文通过引入注入(Injection)、满射(Surjection)和双射(Bijection)的概念,来指导图查询中图模式(G-Pattern)的变异,以便系统地测试图数据库管理系统(GDBMSs)。在这个上下文中,基础查询𝑄被视为域,而变异查询𝑄′被视为陪域。以下是如何利用这些概念来指导G-Pattern的变异:
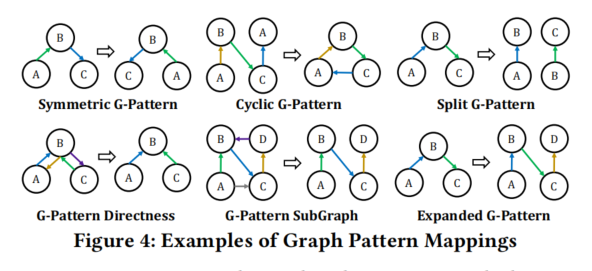
G-Pattern等价(=)
- 双射映射:两个G-Pattern之间的双射映射意味着𝐺𝑃1中的每条边都与𝐺𝑃2中的一条唯一且匹配的边对应,没有任何边被遗漏,使得两个G-Pattern等价。例如,对称G-Pattern、循环G-Pattern和分裂G-Pattern。
G-Pattern限制(≤)
- 满射但非注入:G-Pattern 𝐺𝑃1中的某些边可能不映射到G-Pattern 𝐺𝑃2中。这种映射的例子包括有向G-Pattern和子图G-Pattern,其中通过删除边或节点来生成子图,从而改变了有向边集合成为子集,失去了注入性但保留了满射性。
- G-Pattern限制的例子包括有向G-Pattern和子图G-Pattern,如图4所示。具体来说,G-Pattern的有向性通过删除一个方向来改变无向G-Pattern(例如,𝐺𝑃1={→𝐴𝐵, →𝐵𝐴, →𝐵𝐶, →𝐶𝐵} 和𝐺𝑃2={→𝐴𝐵, →𝐵𝐶});G-Pattern子图可以通过删除边来生成跨度子图,或者通过删除节点及其子集有向边集来生成诱导子图(例如,𝐺𝑃1={→𝐴𝐵, →𝐵𝐶, →𝐶𝐷, →𝐴𝐶, →𝐷𝐵} 和 𝐺𝑃2={→𝐴𝐵, →𝐵𝐶, →𝐶𝐷})。G-Pattern限制将有向边集改变为子集,失去了注入性但保留了满射映射。
G-Pattern泛化(≥)
- 注入但非满射:这种映射类型的例子是G-Pattern限制的逆操作,如扩展G-Pattern,它将有向边集合改变为超集,失去了满射性但保留了注入性。
- 超集
Approach
本方法通过对基础查询应用查询转换来生成等价或变异的变异查询,并进一步检查其结果的预期一致性。直观上,我们的测试神谕是,语义上等价的查询应该获取相同的结果,而变异查询则应该返回更多或更少(至少相等)的结果。图5提供了使用注入式和满射式图查询转换(GQT)的查询转换概览和示例。给定基础查询𝑄,我们利用受注入式和满射式G-Pattern映射启发的查询转换来生成变异查询(例如,𝑄=○1, 𝑄<2○, 𝑄<○=○3)。通过这些操作符,我们可以推断出它们的结果关系,从而通过检查基础查询与变异查询之间的一致性来反映逻辑错误。

本文将图查询转换(Graph Query Transformation, GQT)规则分为三个主要类别,根据它们的策略和作用于图模式(G-Pattern)的不同方式进行分类:结构GQT(G#)规则、属性GQT(H#)规则和非GQT(#)规则。下面是这些规则的详细介绍:
结构GQT(G#)规则(等价)
- 这组规则基于第3节提到的注入式和满射式路径映射,改变图模式同时保留有向边集映射上的注入或满射,或两者。
- 例如,通过应用基于对称G-Pattern映射的转换,从基础查询𝑄变异出等价查询𝑄=○1,这显示了如何在保持结构映射的同时改变图模式。
- 这类规则包括对称模式、展开循环模式、模式分割、添加边方向、生成跨度子图、生成诱导子图和扩展模式等转换。
属性GQT(H#)规则(<=)
- 源于标签属性图模型,这组规则利用节点标签、边类型及其属性来生成注入式和满射式G-Pattern映射,扩大查询转换的空间。
- 一个属性GQT规则的例子是通过添加边类型(例如,[:rated])从基础查询𝑄变异出查询限制𝑄<○2,这考虑到边类型的满射式映射,将有向边集分为两个不相交的子集。
- 这类规则包括添加节点标签、添加边类型、移动标签谓词、计数ID属性和计数其他名称等转换。
非GQT(#)规则(>=)
- 这组规则来源于查询语法或除G-Pattern外的其他查询元素,不显式变异G-Pattern也不使用G-Pattern映射。
- 包括将谓词分为两部分的DisjointPredicate、添加总是为真的条件的RedundantPredicate、更改变量名的RenameVariables和以调用函数方式执行图查询的AddCallWrapper等规则。
- 通过规则组合,这组规则有助于生成多样化的变异查询。
变异算子

Evaluation
在本节中,我们通过回答以下研究问题来评估GraphGenie在各个重要方面的表现:
- Q1 未知错误的发现:GraphGenie在发现成熟GDBMS中的未知错误方面有多有效?
- Q2 与现有技术的比较:GraphGenie在GDBMS测试方面的有效性与最新技术(如Grand和GDBMeter)相比如何?
- Q3 GQT贡献分析:各个规则类别对GraphGenie性能的贡献程度如何?
- Q4 检测性能问题的适用性:GraphGenie是否也适用于发现GDBMS中的性能问题?
目标GDBMS
我们主要测试了使用Cypher的GDBMS,因此在评估中我们专注于它们。我们首先选取了三个排名靠前的Cypher GDBMS来评估GraphGenie的有效性,包括Neo4j、RedisGraph和AgensGraph。表2显示了这些GDBMS的DB-Engine排名、GitHub星标、初始发布日期和代码行数(LoC)。我们还将我们的方法应用于三个使用Gremlin的GDBMS,包括TinkerPop、JanusGraph和HugeGraph,与现有工作进行比较,以展示该方法对其他图查询语言的通用性。
测试数据集
我们使用了Neo4j创建的两个标准数据集,即CyberSecurity和Recommendation。CyberSecurity包含来自活动目录环境审计的数据以及使用图分析可能的攻击路径,包括953个节点和4,858个关系。Recommendation是电影评论的数据集,包含28,863个节点和166,261个关系。
这个评估部分旨在全面检验GraphGenie工具在实际应用中的有效性和适用性,通过对成熟的GDBMS进行测试,以及与现有技术的比较,来展示其在发现未知错误和性能问题方面的能力。同时,通过分析不同规则类别的贡献,进一步理解GraphGenie性能的关键因素。
