SMT Solver Validation Empowered by Large Pre-trained Language Models

ABSTRACT

SMT求解器已被用于检验逻辑公式的可行性，并已应用于多个关键领域，包括软件验证、测试用例生成和程序合成。然而，隐藏在SMT求解器中的错误可能导致严重的后果，引发SMT求解器中的错误结果。因此，确保SMT求解器的可靠性和健壮性至关重要。尽管已提出了多种测试方法用于SMT求解器，生成有效的测试公式对于全面测试SMT求解器仍是一项挑战。为了解决这一挑战，本研究提出将大型语言模型（LLMs）用于生成用于模糊测试SMT求解器的SMT公式。具体而言，本研究提出了一种新的重训细调流程来释放语言模型生成有效SMT公式的潜力，并通过数据增强提高其生成性能。我们将该方法实现为一个实用的模糊测试工具，名为LAST，并对当前最先进的SMT求解器，即Z3、cvc5和Bitwuzla进行了广泛测试。迄今为止，LAST已成功揭示了65个真实错误，其中45个已被开发者修复。

INTRODUCTION

Background

  1. SMT求解器概述:
    • 定义：高级自动定理证明工具，检验特定理论中一阶逻辑公式的可满足性。
    • 应用：广泛用于软件验证、程序合成、程序分析等领域。
  2. SMT求解器的重要性:
    • 影响：求解器的质量直接影响其应用的可靠性和效率。
    • 实例：亚马逊每天调用数百万次SMT求解器进行服务访问控制。
  3. 测试SMT求解器的方法:
    • 主要策略：公式生成和公式变异。
      1. 公式生成:
        • 工具例子：FuzzSMT, Murxla。
        • 方法：使用预定义策略从零开始生成测试公式。
      2. 公式变异:
        • 工具例子：YinYang, STORM, OpFuzz, TypeFuzz, HistFuzz。
        • 方法：通过变异现有公式来产生新的测试实例。
          • YinYang：结合两个具有相同可满足性的公式生成更复杂的公式。
          • STORM：将种子公式分割成多个子公式并重新组合生成满足条件的变异体。
          • OpFuzz：变异公式中的操作符。
          • TypeFuzz：扩展变异空间，生成新的公式片段。
          • HistFuzz：利用历史错误触发公式中的元素生成有效变异体。
  4. 技术挑战:
    • 变异空间限制：导致测试效果可能受限。
    • 数据利用不足：HistFuzz虽使用历史错误数据，但方法基础，许多有价值的线索未被充分利用。

Limitations

这段文本探讨了设计有效的SMT求解器测试公式的挑战以及大型预训练语言模型（LLMs）的潜在应用。以下是关键点的概括：

  1. 挑战:
    • 设计有效的SMT求解器测试方法是一项具有挑战性的任务。
    • 即使是经验丰富的SMT求解器专家也可能无法充分发掘历史错误触发公式和求解器特有行为中的有效元素。
    • 仅依赖人工编写的测试公式或独立技术生成的公式不足以全面验证SMT求解器。
  2. 预训练语言模型的应用:
    • 大型预训练语言模型（LLMs）在各种自然语言和编程语言任务（例如代码理解、程序修复和编译器测试）上表现出色，提供了解决测试公式缺失挑战的有希望的方法。
    • SMT公式具有高度专业化的语法和严格的规则，尽管与自然语言和编程语言不同，但展现了一定的“自然性”，因此LLMs有望有效生成SMT公式。
  3. 存在的问题和限制:
    • 当前缺乏经验证据支持LLMs在生成测试公式方面的有效性。
    • 获取高质量的SMT公式生成训练数据几乎不可行，这也是将预训练的LLMs成功迁移到原始领域之外的一个重大挑战。

Approach

这段文本描述了利用大型预训练语言模型（LLMs）改进对SMT求解器测试的方法，主要包括两个步骤：重训练和微调。

  1. 重训练:
    • 目的是让LLMs能够在特定于SMT的语料库上生成准确的公式。
    • 通过收集标准规范的SMT公式作为训练数据，确保生成的公式符合SMT求解器的标准。
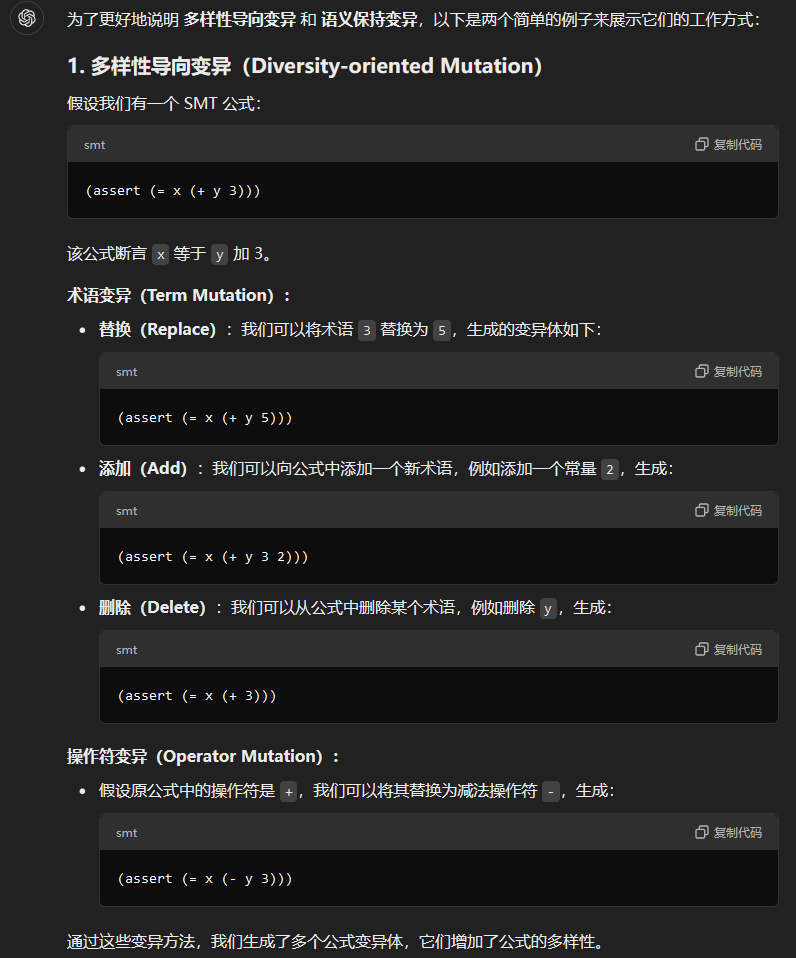
    • 引入多样性导向的变异方法，包括术语变异和操作符变异，以从现有公式中创造出不同的新公式，这有助于模型生成更多能够触发求解器错误的测试公式。
  2. 微调:
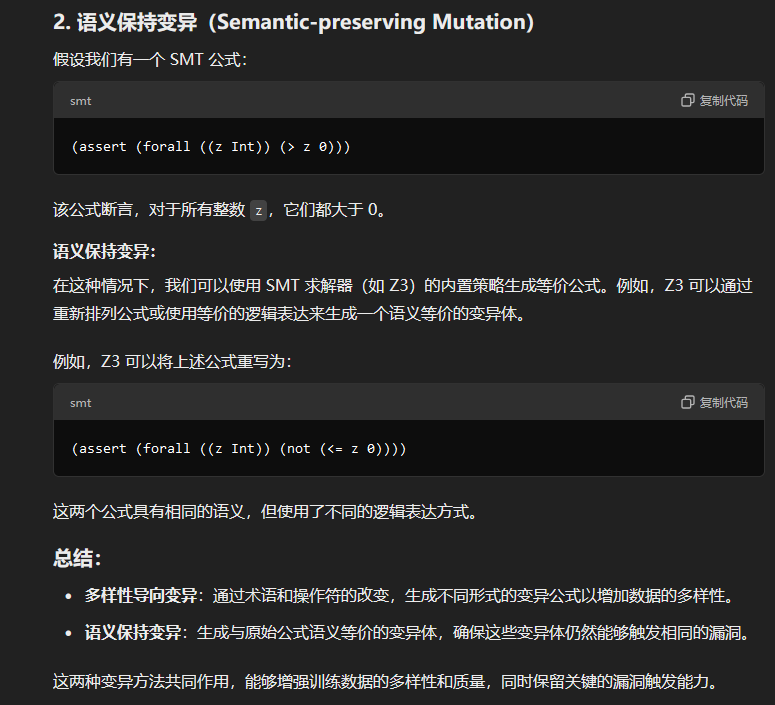
    • 采用语义保持变异策略，保证变异后的公式在语义上与原公式等效，从而能够触发相同的错误。
    • 利用SMT求解器Z3的功能进行语义等效变换，生成足够的触发错误的公式。
    • 这一步骤旨在指导LLMs生成更有效的测试公式，增加发现求解器潜在错误的概率。

这种方法通过系统的重训练和精确的微调，旨在构建一个强大的LLM，能够生成用于测试SMT求解器的有效和多样化的测试公式。

Result

  • 工具实现：
    • 实现了名为 LAST 的SMT求解器测试工具，基于GPT-2模型。
    • 评估了LAST在三个SMT求解器（Z3、cvc5、Bitwuzla）上的效果，共报告65个漏洞，其中45个已被修复。
  • 主要发现：
    • LAST能够生成大量有效的公式，显示出LLMs（大语言模型）在生成超出传统自然语言和编程语言的内容上的有效性。
    • LAST生成的测试公式具有高代码覆盖率，并且在bug检测方面展示了较强的能力。
  • 贡献：
    1. 原创性：
      • 提出了一种新的 retrain-finetune 管道，重定向LLMs生成多样化的公式以进行SMT求解器的压力测试。
      • 这是首次将LLMs应用于SMT求解器验证的工作，提供了LLMs有效性的实证依据。
    2. 新颖性：
      • 引入了两个策略：
        • 多样性导向变异（diversity-oriented mutation）
        • 语义保持变异（semantic-preserving mutation）
      • 这些策略丰富了用于LLMs再训练和微调的数据，提高了SMT公式的生成效果。
    3. 重要性：
      • 目标是识别SMT求解器中的真实漏洞，证明LLMs可以生成超出典型自然语言和编程语言的内容，具有未来研究潜力。
    4. 实用性：
      • 报告了三个高级SMT求解器（Z3、cvc5、Bitwuzla）的65个漏洞，其中45个已被开发者修复。
      • 评估结果显示，LAST工具对现有SMT求解器模糊测试技术具有补充作用。

BACKGROUND AND MOTIVATION

A. SMT-LIB Language

SMT-LIB语言：SMT-LIB 是广泛用于 SMT 求解器的输入语言，采用该语言的求解器数量众多。其规范定义了多种命令，用于不同目的。基本命令包括 declare-fun、assert 和 check-sat。

  • declare-fun 命令：用于声明新的符号。
  • assert 命令：将公式添加到断言栈，表示需要求解的问题。
  • check-sat 命令：用于询问求解器断言栈中的公式是否可满足，返回 sat（可满足）或 unsat（不可满足）。

基本概念：

  • 操作符与项：是 SMT 公式的基本构建块。预定义的函数符号（如 +、-、*、/）是操作符。项 是表示特定类型值的语法表达式。
  • 项的结构：项可以是常量、变量、函数符号或限定符，如全称量词 forall 和存在量词 exists。

实例说明：给出了一个 SMT-LIB 实例，说明了如何使用 declare-fun 和 assert 命令来声明变量和构建公式。

image-20241019200802040

变量声明：

  • (declare-fun x () Bool)：声明了一个名为 x 的布尔变量，表示 x 的值是 true 或 false。
  • (declare-fun y () Real)：声明了一个名为 y 的实数变量，表示 y 的值是一个实数。

断言公式：

  • (assert (forall ((z Real)) (= x (< z y)))) ：
    • 这个 assert 语句将一个量化公式加入断言栈中。
    • forall ((z Real))：表示对所有实数 z，公式中的条件都必须成立。
    • (= x (< z y))：公式断言 x 等于 z < y 的结果，即 x 的值为 z 是否小于 y 的布尔结果。如果 z 小于 y，则 x 为 true，否则 x 为 false。

可满足性检查：

  • (check-sat)：这是一个标准的SMT-LIB命令，表示求解器需要检查当前断言栈中的公式是否可以满足。
    • 求解器将返回 sat（可满足）或 unsat（不可满足），这取决于是否存在一组 x、y、z 的值使得所有断言成立。

B. Large Pre-trained Language Models

大型预训练语言模型（LLMs）：

  • LLMs 的基本原理：通常是基于 Transformer 的神经网络，通过预测句子中下一个词来学习语言的结构和模式。这使得LLMs可以在没有特定任务目标的情况下，从大量文本中学习语言的普遍结构。
  • 微调与下游任务：LLMs 可以在更小且更具体的数据集上进行微调，用于文本分类、摘要生成、内容生成等下游任务。LLMs 还可以通过程序数据集的训练，学习不同编程语言的语法和语义，已经成功应用于代码补全和代码总结等任务。
  • 在软件测试中的应用：LLMs 可以生成大量测试用例，在模糊测试（fuzzing）JavaScript 引擎和深度学习库方面也显示了有效性。

生成 SMT 公式的挑战：

  • SMT-LIB 语言的复杂性：SMT-LIB 是一种形式逻辑语言，具有高度专业化的语法和严格的规则，用于表达复杂的逻辑约束。尽管如此，SMT-LIB 语言也表现出一定程度的“自然性”，这意味着LLMs 可以通过学习生成 SMT 公式。
  • 自然性与程序的关系：SMT 公式能够表示程序的约束，表明这些公式与程序的语义紧密相连。根据编程语言的自然性推测，SMT 公式也具有一定的“自然性”，这暗示 LLMs 可能适用于生成 SMT 公式。
  • 挑战与研究目标：尽管这种推测缺乏充分的实证依据，LLMs 的再利用和生成高效 SMT 公式需要高质量的训练数据，而这些数据不易获得。本研究旨在解决这些挑战，并探讨训练 LLMs 以用于 SMT 求解器模糊测试的可行性。

C. Data Augmentation（数据增强）

定义与应用：数据增强是一种广泛使用的技术，通过对原始数据应用各种变换来增加数据集的多样性和规模。这种技术能够提升深度神经网络的泛化能力和鲁棒性。最初，数据增强技术主要应用于计算机视觉领域，通过翻转、旋转、颜色修改等图像变换来增加训练数据的多样性。

扩展到其他领域：最近，数据增强技术的应用扩展到了其他领域，包括代码数据。例如，使用代码转换工具来增强代码数据集的规模，并保持原始代码语义不变。增强的数据集能够提升模型在源代码理解方面的性能。

在SMT公式中的应用：受这些进展的启发，本文提出在SMT公式生成中引入数据增强技术，以解决高质量训练数据有限的问题。通过扩充训练数据集，提高模型的泛化能力，从而在生成有效SMT公式方面获得更好的性能。

APPROACH

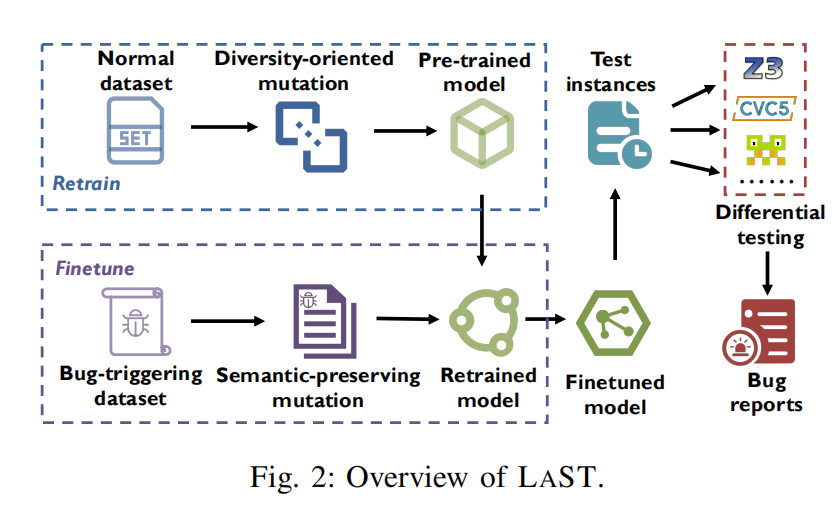
image-20241019201514397

A. Overview

目标：本文提出了一种重新训练-微调（retrain-finetune）管道，旨在通过学习SMT求解器特定知识以及触发漏洞的公式来增强大规模预训练语言模型（LLMs）的能力。

挑战与解决方案：由于缺乏足够的多样化训练数据，本文提出了两种数据增强策略：

  1. 多样性导向的变异策略（diversity-oriented mutation strategy）
  2. 语义保持变异策略（semantic-preserving mutation strategy）

这些策略生成了多样且高质量的训练数据，以帮助重新训练和微调LLMs。

微调过程：首先使用多样性变异增强的公式重新训练LLM，然后进一步微调LLM，使其能够生成触发漏洞的公式。微调时结合使用触发漏洞的公式和语义保持变异生成的公式。

成果：最终，利用训练好的LLM生成大量测试公式，用于对SMT求解器进行模糊测试（fuzzing）。通过检测不同SMT求解器对相同公式的求解结果中的不一致性，LLM能够有效地发现漏洞。

B. Data Collection

LLMs 转换成功的依赖性：LLMs 生成 SMT 公式的成功很大程度上依赖于用于重新训练 LLMs 的训练数据的多样性。因此，收集高质量的训练数据对于有效地重新训练预训练的 LLMs 至关重要。

数据来源：SMT-LIB 提供了官方的SMT求解器基准测试集，其中包含数千个严格遵循规范的公式。大多数这些公式来源于实际应用或用于评估性能，通常不会触发 SMT 求解器中的漏洞。开源 SMT 求解器（如 Z3 和 cvc5）的 bug 跟踪系统中包含了触发漏洞的公式，这些公式可以从系统中提取以进行训练。

数据增强工具：使用 HistFuzz 工具来收集这些触发漏洞的公式，这些公式包含大量的特定求解器知识，未在之前的研究中得到充分利用。

训练数据筛选：为了确保数据适合 LLMs，过滤掉了过长的公式（超过 LLMs 上下文窗口的限制）。例如，GPT-2 的限制是 1024 个 token。一般来说，bug 触发公式较短，90% 的公式小于 5KB，因此也排除了超过 5KB 的公式。 Bug触发的公式较短

数据集规模：最终收集了 139,367 个用于重新训练 LLM 的公式，以及来自 Z3 和 cvc5 的 3,474 个 bug 触发公式用于微调。

数据格式化：在数据增强之前，对公式进行了重构和统一格式化。具体来说，移除了 let 绑定符号，并根据变量的类型重命名变量（例如，将 x 和 y 分别重命名为 bool_0 和 real_0）。

C. Augmentation for Training Data

目的：为了解决微调数据集相对较小的问题，本文通过数据增强技术来提高训练数据的数量和多样性。

多样性导向变异：

  • 介绍了两种变异策略：术语变异和操作符变异。
  • 术语变异：通过替换、添加或删除公式中的术语来生成变异体。例如，术语可以通过不同的转换函数（如 to_real 或 str.to_int）进行转换，以确保类型一致性。
  • 操作符变异：用与原始操作符有相同操作数和返回值类型的操作符替换原操作符，从而生成变异体。每个基准测试中的每个公式随机生成 10 个变异体，总共生成超过一百万个变异体。

语义保持变异：

  • 采用 SMT 求解器 Z3 的内置策略来生成语义等价的变异体，从而确保变异体保留漏洞触发能力。
  • 通过过滤冗余和重复的变异体，最终从 bug 触发公式中收集了 19,062 个变异体。

数据增强效果：通过这些数据增强策略，生成了大量的变异体，显著扩展了训练数据集的规模和多样性，从而有助于提高 LLM 的整体性能。这些增强数据能够帮助模型学习大量 SMT 公式知识，进而生成新的测试公式以揭露漏洞。

image-20241019203016494

image-20241019203108345

D. Test Formula Generation

模型使用：

  • LAST 使用 OpenAI 提供的 GPT-2 语言模型，该模型经过大量自然语言数据的预训练。
  • 为了生成 SMT 公式，首先通过 Byte Pair Encoding (BPE) 对公式进行分词，将每个 SMT 公式中的命令、符号、常量等分解为子词或字符，并映射为整数值，构建词汇表。

模型重训练：

  • 通过使用基准公式及其多样性导向变异版本，对 GPT-2 模型进行重训练。
  • 重训练使用 Adam 优化器，在 150,000 次迭代和初始学习率 0.0001 下进行，并使用两块 NVIDIA RTX 3080 Ti GPU。

模型微调：

  • 重训练完成后，使用漏洞触发公式及其变异体进行微调，以捕捉漏洞触发元素并纳入求解器的特定知识。
  • 微调采用与重训练相同的设置，但只更新模型中最后两层的全连接层权重，训练 50,000 次迭代。

测试输入实例化：

  • 一旦模型完成训练，可以生成新的测试公式。通过空提示符生成一系列 token，并选取其中最长的完整公式作为测试输入。
  • 生成公式时使用温度参数 0.7 控制模型的创造性，由于生成的公式不一定完整，最后会对不完整的公式进行修正，确保它们能够被 SMT 求解器正常执行。

E. Differential Testing

目的：为了发现 SMT 求解器中的漏洞，采用了差分测试方法，即比较多个 SMT 求解器在相同测试公式上的结果。

方法：

  1. 如果一个求解器返回 sat，而另一个求解器返回 unsat，则认为这可能是一个潜在的健全性漏洞。通过使用 get-model 命令获取使公式满足的模型来确定哪个求解器出现了问题。
  2. 如果模型可以评估为 sat，则将返回 unsat 的求解器视为存在健全性漏洞，反之亦然。
  3. 为避免误报，排除 SMT-LIB 规范不足导致的不同求解器行为差异的情况。
  4. 还通过模型检查是否能正确评估为 sat，如果不能，则认为是无效模型漏洞。
  5. 如果求解器出现异常行为（如断言失败），则记录为崩溃漏洞。

报告：经过手动检查后，报告已识别的漏洞给相关求解器的 bug 跟踪系统。

EVALUATION

研究问题：

  • RQ1: LAST 是否可以生成有效的 SMT 公式？
  • RQ2: LAST 能否用于揭示 SMT 求解器中的真实漏洞？
  • RQ3: LAST 是否能够补充最先进的 SMT fuzzers？
  • RQ4: LAST 的主要组件有多大效果？

漏洞类型：

  • 健全性漏洞（Soundness bugs）：当两个求解器对同一个公式给出相反结果（一个返回 sat，另一个返回 unsat）时，认为存在健全性漏洞。
  • 无效模型漏洞（Invalid model bugs）：求解器错误地将某个公式判断为 sat，但提供的模型无法满足公式的约束条件。
  • 崩溃漏洞（Crash bugs）：当求解器在求解过程中出现异常行为（如断言违规或段错误）时，认为存在崩溃漏洞。

实验环境：

  • 实验运行在具有 40 核心 Intel Xeon CPU Gold-6230 和 128GB 内存的 Ubuntu 20.04 系统上。使用 AddressSanitizer 工具识别和去重崩溃（如内存泄漏和自由后使用漏洞）。每个公式的求解时间限制为 10 秒。

A. RQ1: Validity of Generated Formulas

实验设置：

  • 公式被认为是有效的，前提是它可以通过 Z3 或 cvc5 求解且不出现任何错误。
  • Z3 和 cvc5 是两个被广泛应用于评估的成熟 SMT 求解器，支持多种逻辑。
  • 实验生成了 1,000 个公式，在不同温度下使用 Z3 和 cvc5 进行测试。温度从 0.1 到 1.0，间隔为 0.1。
  • 通过计算在不同温度下生成的有效公式的比例来评估公式的有效性。

实验结果：

  • 当温度设置在 0.2 到 0.7 之间时，LAST 生成有效公式的比例较高，超过 60%。
  • 在 0.2 的温度下，81% 的公式是有效的，达到最高比例。
  • 这些结果表明训练后的模型可以在适当的温度范围内生成有效公式。
  • 为了在确保高创造性的同时生成有效公式，实验建议将温度设置为 0.7。

B. RQ2: Bug Detection

image-20241019204243523
  1. 实验目标：
    • RQ2的目标是验证LAST能否检测出SMT求解器中的真实bug，这是衡量LAST有效性的重要指标。
  2. 实验设置：
    • 目标求解器：实验中选择了Z3、cvc5和Bitwuzla作为目标求解器。
      • Z3和cvc5是社区中广泛使用的SMT求解器，支持广泛的逻辑功能。
      • Bitwuzla是一个相对较新的SMT求解器，由cvc5的开发者推荐，其在某些特定逻辑领域表现强大。
    • 选项选择：实验集中于求解器的默认模式，同时启用一些必要的选项来检测模型错误和其他潜在问题。
  3. Bug检查与减少：
    • 为了避免误报，研究采用了一些策略来减少bug报告的重复性。
    • 使用分组方法将可能的相关bug归类为一个问题，并对bug进行去重和简化处理。
    • 通过工具如ddsMT和Delta来减少公式的大小，使之更容易理解和修复。
  4. 结果：
    • 表格显示了在Z3、cvc5和Bitwuzla中发现的65个bug的状态，其中45个已经被开发者修复。
    • 在修复的bug中，大部分是崩溃类型的bug，少数是无效模型和可靠性问题。
    • 其中一些bug在Z3和cvc5中已潜伏多年，表明LAST可以揭示长期未被发现的bug。LAST甚至将测试实例提交给Z3的测试仓库，已被开发者采纳，进一步展示了这些bug的重要性。

这段内容展示了LAST对SMT求解器的有效bug检测能力，尤其是检测出长期潜在的bug，并表明LAST对提高求解器的可靠性有显著作用。

C. RQ3: Complementarity Analysis

RQ3的目标是研究LAST是否能够从以下两个方面补充现有的SMT模糊测试工具：

  1. 代码覆盖率：通过生成的公式所实现的代码覆盖范围。
  2. 暴露Bug的能力：生成公式揭露bug的能力。

实验设置：

  • 基线工具：实验比较了LAST与其他前沿的SMT模糊测试工具（如YinYang、STORM、OpFuzz、TypeFuzz和HistFuzz），所有这些工具均开源，并使用最新版本及默认配置进行测试。
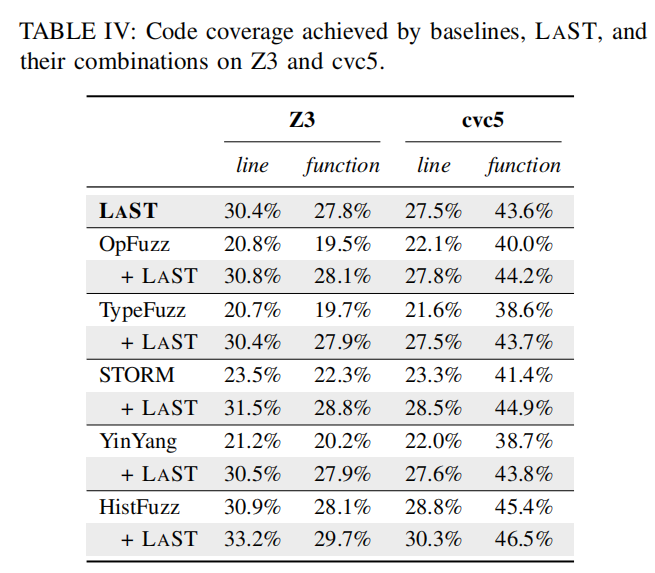
  • 代码覆盖率：通过从SMT-LIB基准中随机抽取100个公式，并利用这些工具生成1000个变异公式进行测试，最后使用gcov工具收集求解器的代码覆盖率。结果表明，LAST的代码覆盖率在Z3和cvc5上的表现优于其他基线工具，尤其是当LAST与其他工具结合使用时，覆盖率会进一步提升。
  • Bug揭露能力：每个模糊测试工具在24小时内运行，并记录所找到的唯一bug数量。LAST通过纠正提交的方法验证bug的有效性。结果显示，LAST在同一时间内比其他模糊测试工具发现了更多bug，尤其是能找到基线工具未能检测到的bug。

结果：

  • 代码覆盖率：LAST在Z3和cvc5上的代码覆盖率分别为30.4%和27.5%，显著超过其他模糊测试工具。当LAST与其他模糊测试工具结合使用时，代码覆盖率进一步提升到33.2%。
  • image-20241019204822295
  • Bug揭露能力：在已知的六个bug中，LAST在24小时内发现了其中的五个，而基线工具如STORM在相同时间内未能发现任何bug。特别是，对于最新版本的求解器，LAST揭露了Z3和cvc5中的多个长期潜伏的bug。
image-20241019204755408

D. RQ4: Ablation Study

RQ4 研究了LAST各个组成部分对其有效性的贡献，主要关注微调过程和数据增强技术。

实验设置：

  • 进行了消融实验，测试了两种变体：
    1. LAST-woFT：不包含微调过程。
    2. LAST-woDF：不包含数据增强和微调过程。

实验与RQ3相同，主要比较代码覆盖率。

结果：

  • LAST-woFT 的代码覆盖率比完整的LAST低，说明微调过程有助于提高代码覆盖率。
  • LAST-woDF 的覆盖率进一步降低，表明数据增强技术也对提高代码覆盖率有显著贡献。

结论：

微调过程和数据增强技术均对提高LAST的代码覆盖率有重要作用，两个过程共同提升了LAST的有效性。