Finding Logic Bugs in Spatial Database Engines via Affine Equivalent Inputs

Abstract

空间数据库管理系统（SDBMSs）旨在存储、操作和检索空间数据。SDBMSs 被广泛应用于现代各类应用中，例如地理信息系统、计算机辅助设计工具和基于位置的服务。然而，SDBMSs 中存在逻辑错误可能导致错误的结果，极大地削弱这些应用的可靠性。在 SDBMSs 中检测逻辑错误非常具有挑战性，因为缺乏用于识别错误结果的真实基准。在本文中，我们提出了一种自动几何感知生成器，用于为 SDBMSs 生成高质量的 SQL 语句，并引入了一个新的概念仿射等价输入 (AEI) 来验证 SDBMSs 的结果。我们将这些概念实现为一个名为 Spatter (Spatial DBMSs Tester) 的工具，用于检测四种流行 SDBMSs 中的逻辑错误：PostGIS、DuckDB Spatial、MySQL 和 SQL Server。我们的测试活动检测到了 34 个之前未知且独特的错误，其中已有 30 个得到确认，18 个已被修复。我们的测试工作得到了开发人员的高度赞赏。实验结果表明，几何感知生成器在检测独特错误方面远远优于简单的随机形状生成器，AEI 能够识别出 14 个被之前方法忽略的 SDBMSs 逻辑错误。

INTRODUCTION

Background

SDBMS的定义和功能

空间数据库管理系统（SDBMSs）旨在存储、操作和检索空间数据，这些数据描述了坐标系统下的对象和位置。

SDBMS的应用场景

地理信息系统（GIS）
计算机辅助设计（CAD）
基于位置的服务（LBS）
科学模拟

SDBMS的实现形式

作为广泛使用的关系型数据库的空间扩展或内置功能：
- PostGIS：PostgreSQL 的空间扩展。
- MySQL：支持内置的空间功能。

SDBMS可靠性问题

尽管 SDBMSs 很重要，但其可靠性没有受到足够重视。

现有方法的局限性

一般用途的fuzzers 已用于检测导致崩溃的输入（即崩溃错误），但未能检测逻辑错误。
崩溃错误：导致系统进程终止，容易被发现。
逻辑错误：导致计算结果错误，但不会中断程序运行，往往被开发人员和用户忽视。

Motivating example

问题描述

在 PostGIS 中，插入了一条线段和一个点，并查询线段是否覆盖该点。
查询使用的 SQL 语句见 Listing 1 和 Listing 2，其中 ST_Covers 用于判断覆盖关系。

实际情况

在图 1(a) 中，线段和点的关系清晰显示：线段确实覆盖了该点，因此正确的结果应该是 1。

PostGIS 返回错误结果

PostGIS 返回了 0，即表示线段没有覆盖点，这与实际情况不符，揭示了一个逻辑错误。

仿射等价示例

在 Listing 2 中，几何体经过仿射变换（图 1(b)），但保持了与原始几何体等价的覆盖关系。
这次查询返回了正确的结果 1，说明仿射变换下可以检测出逻辑错误。

示例意义

通过这一示例揭示了 PostGIS 在特定情况下的逻辑错误，强调了仿射等价输入（Affine Equivalent Inputs, AEI）在检测此类错误中的有效性。

精度问题导致错误：

在 Listing 1 中，点的坐标计算过程中出现顶点归一化（即位移到原点）时的精度损失。
Listing 2 中，由于点正好位于原点，避免了位移计算，未触发此错误。

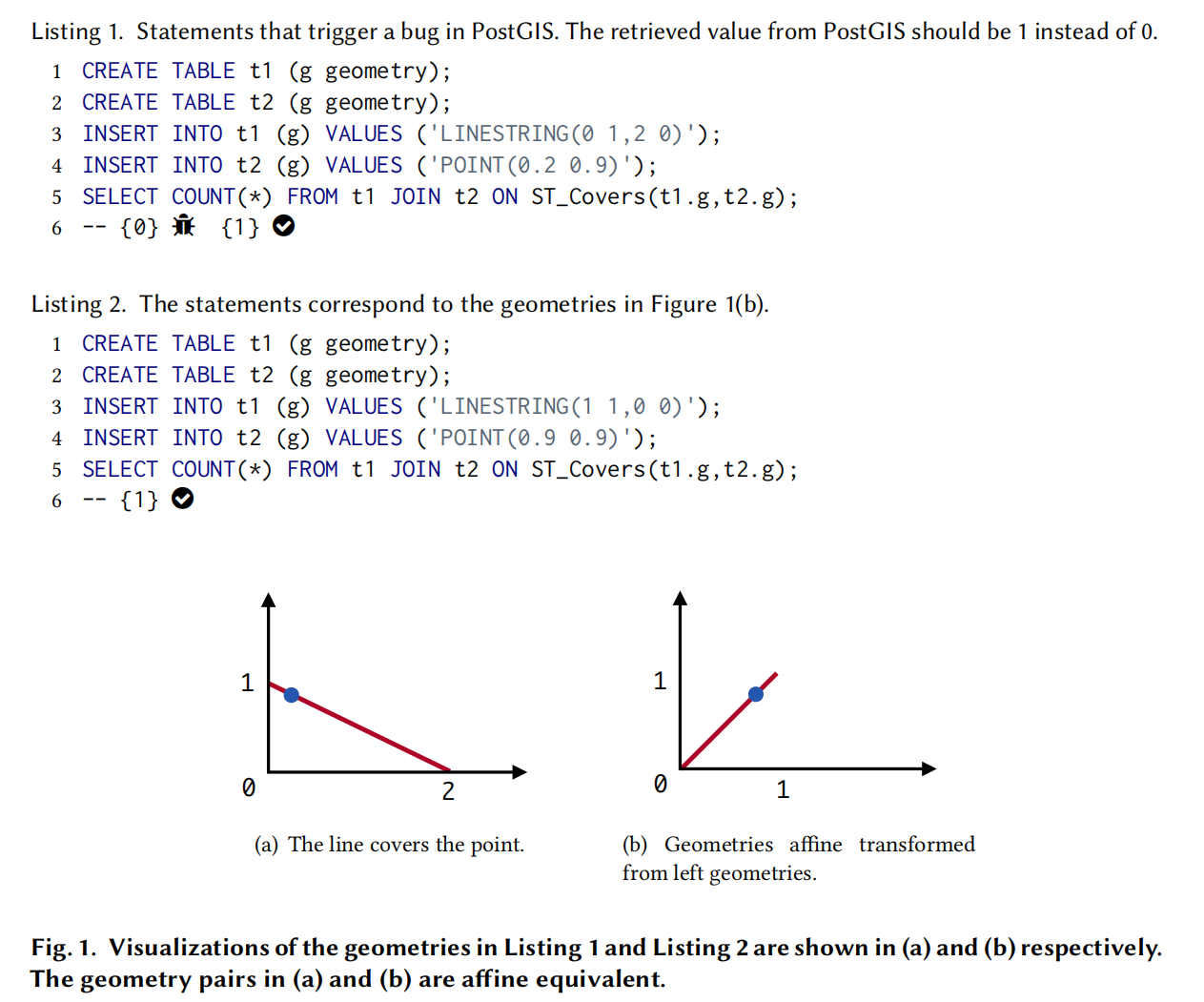
没有解释清楚是怎么进行变换的

Existing or potential approach

自动检测 SDBMS 逻辑错误的挑战

过去主要依赖用户报告来发现逻辑错误，缺乏自动化测试策略。
核心挑战：缺乏结果的真实基准，难以验证输出是否正确。

现有方法的局限性

差分测试：
- 比较多个系统的查询输出结果，推断正确结果。
- 局限性：
  - 空间相关功能通常只在单一 SDBMS 中实现，无法应用差分测试。
  - 共享第三方库可能导致多个系统产生一致但错误的结果，导致错误被忽略。
  - 标准化限制：尽管 OGC 标准存在，但 SDBMS 实现细节不同，导致输出结果存在预期的不一致性。
- 示例：ST_Covers 函数仅在 PostGIS 和 DuckDB Spatial 中实现，无法使用差分测试检测。
三值逻辑分区（TLP）：
- 通过将原始查询分割成三个子查询，并验证其结果之和是否等于原查询的结果。
- 局限性：
  - 对于空间相关功能，TLP 无法检测到逻辑错误，因为原始查询和分区查询的结果均为错误。
- 示例：Listing 1 中的逻辑错误无法被 TLP 检测。

必要性

现有自动化测试技术无法有效应用于 SDBMS，特别是空间相关功能。
需要一种面向 SDBMS 的新方法，用于生成测试用例和期望结果，从而自动检测逻辑错误。

这个分类不是很make sense，TLP 只是 metamorphic testing 的一种

Key insight

提出方法

提出一种名为 Affine Equivalent Inputs (AEI) 的方法，用于为 SDBMS 提供预期结果。

核心洞察

两个几何体如果通过仿射变换（例如旋转、缩放、平移）保持一致，则它们的拓扑关系（如相交、覆盖、不相交）也应保持不变。

检测逻辑错误

若 SDBMS 对两组仿射等价几何体返回的拓扑关系不一致，则可以检测出一个逻辑错误。

仿射等价定义

两个几何体在仿射变换下可以相互转换，则称它们为仿射等价。

Evaluation and contributions

工具设计

基于 AEI，开发了名为 Spatter 的自动化测试工具，用于检测 SDBMSs 的逻辑错误。
Spatter 包括：
- 几何感知生成器：生成高质量 SQL 语句。
- 使用 AEI 验证 SDBMSs 的查询结果。

测试目标与效果

选取了 4 个广泛使用的 SDBMSs 进行测试：PostGIS、MySQL、DuckDB Spatial 和 SQL Server。
主要成果：
- 检测到 34 个 之前未知且独特的错误。
- 其中 30 个 已被确认，18 个已修复，20 个属于逻辑错误。
- AEI 识别了 14 个 被现有方法忽略的逻辑错误。

工具评价

Spatter 显著优于基线策略（如随机形状生成器）在检测独特错误方面的性能。
得到了 SDBMS 开发者的积极反馈。

主要贡献

提出了 Affine Equivalent Inputs (AEI) 方法，用于自动验证 SDBMSs 结果。
设计并实现了自动化测试工具 Spatter。
在四个流行 SDBMSs 中检测出 34 个 之前未知的错误。
通过评估证明 Spatter 优于现有测试方法。

Background

在本节中，我们将提供关于几何类型、拓扑关系查询和仿射变换的重要背景信息。

2.1 Geometry Types

几何类型的重要性

SDBMS 提供的几何类型被广泛应用于实际数据集，并支持多种操作功能。
这些几何类型遵循 OGC 标准（Open Geospatial Consortium）。

基本几何类型（左侧示例）

POINT：维度为 0。
LINESTRING：维度为 1。
POLYGON：维度为 2。

扩展几何类型

MULTI 几何：由相同基本类型的多个元素组成，例如 MULTIPOINT、MULTILINESTRING 和 MULTIPOLYGON。
MIXED 几何：混合多种不同的几何类型，例如 GEOMETRYCOLLECTION。

总结

基本几何类型和扩展类型（MULTI 和 MIXED）是 SDBMS 支持的重要数据结构，图 2 展示了这些类型的示例。

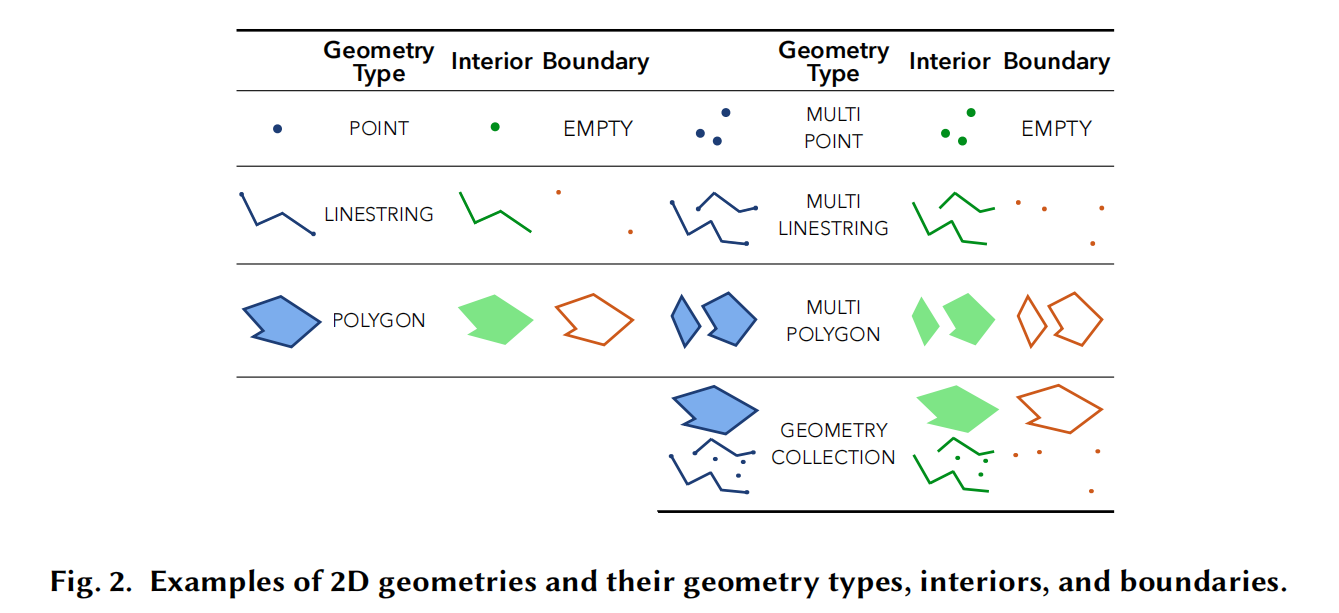
2.2 Topological Relationship Queries

拓扑关系的重要性
- 拓扑关系描述了空间对象之间的相对位置，是 SDBMS 中空间查询和连接操作的核心功能。
- 确保拓扑关系查询的正确性对于 SDBMS 至关重要。
拓扑关系的分类
- 正式拓扑关系：
  - 基于 维度扩展的 9 交模型 (DE-9IM) 定义。
  - 将几何体抽象为单元复合体（cell complexes），通过单元的边界、内部和外部计算关系。
  - 使用 3×3 矩阵来表示两几何体之间的关系，矩阵中的值通过维度计算器 (D) 得出。
  - 示例：PostGIS 中的 ST_Relate(g1, g2) 函数基于 DE-9IM 实现，输出长度为 9 的字符串，如 FF21F1102。
  - 1. 正式拓扑关系 (Formal Topological Relationships)
    - 基于 DE-9IM (Dimensionally Extended 9-Intersection Model) 定义，通过计算两个几何体之间的边界、内部和外部的交集，形成一个 3×3 矩阵。
    - 结果以长度为 9 的字符串表示，每个字符表示交集的维度或状态：
      
      F：空集
      
      0：点
      
      1：线
      
      2：面
    示例：ST_Relate
    假设有两个几何体：
    - **几何体1 (g1)**：一条线段。
    - **几何体2 (g2)**：一个多边形。
    计算这两个几何体的拓扑关系：
    1
    2
    3
    4
    5
    SELECT ST_Relate(
    ST_GeomFromText('LINESTRING(0 0, 2 2)'),
    ST_GeomFromText('POLYGON((1 1, 3 1, 3 3, 1 3, 1 1))')
    );
    解释：ST_Relate 返回结果类似于 **”FF21F1102”**。
    - 代表：线段与多边形的内部、边界、外部的交集情况。
    - 例如，2 表示交集是一个面，1 表示交集是一条线，F 表示没有交集。
- 命名拓扑关系：
  - 从正式拓扑关系派生而来，更易于用户理解。
  - 常见的命名拓扑关系包括 ST_Disjoint 和 ST_Intersects。
  - SDBMS 还提供特定功能，如 PostGIS 和 DuckDB Spatial 中的 ST_Covers。
  - 2. 命名拓扑关系 (Named Topological Relationships)
    - 从正式拓扑关系派生而来，具有更直观、易于理解的名称。
    - 每个命名关系函数通过某种条件来判断两个几何体之间的拓扑关系，返回 TRUE 或 FALSE。
    示例：ST_Intersects 和 ST_Covers
    1. ST_Intersects：判断两个几何体是否相交。
    1
    2
    3
    4
    5
    SELECT ST_Intersects(
    ST_GeomFromText('LINESTRING(0 0, 2 2)'),
    ST_GeomFromText('POLYGON((1 1, 3 1, 3 3, 1 3, 1 1))')
    );
    结果：TRUE
    
    解释：线段与多边形有交集，返回 TRUE。
    1. ST_Covers：判断一个几何体是否完全覆盖另一个几何体。
    1
    2
    3
    4
    SELECT ST_Covers(
    ST_GeomFromText('POLYGON((0 0, 4 0, 4 4, 0 4, 0 0))'),
    ST_GeomFromText('POINT(2 2)')
    );
    结果：TRUE
    
    解释：多边形完全包含点 (2 2)，返回 TRUE。
DE-9IM 模型核心概念
- 单元复合体由不同维度的单元（cells）构成：
  - 0-单元：点。
  - 1-单元：线段。
  - 2-单元：多边形。
- 边界、内部和外部定义：
  - 单元的边界为其低维元素，内部为闭包减去边界，外部为全局集合减去闭包。
- 示例：图 3 展示了两几何体的拓扑关系，通过其边界和内部的交集计算得出矩阵值。
问题与挑战
- 拓扑关系查询在实际应用中被广泛使用，但当前缺乏通用的测试方法来检测逻辑错误。
- 现有方法未能覆盖这些查询的复杂性和正确性验证，导致潜在错误被忽略。

总结：拓扑关系分为正式拓扑关系（基于 DE-9IM）和命名拓扑关系，两者广泛应用于 SDBMS 中。然而，当前尚无自动化方法来测试和验证这些拓扑关系查询的正确性，亟需解决该问题。

正式拓扑关系：通过 DE-9IM 矩阵提供详细的几何交集信息，适合复杂分析。
- 示例：ST_Relate，返回详细的字符串表示。
命名拓扑关系：提供直观易懂的判断结果，适合用户查询和理解。
- 示例：ST_Intersects、ST_Covers，返回布尔值 (TRUE 或 FALSE)。

2.3 Affine Transformations

仿射变换的概念

仿射变换是一种数学和计算机图形学中的基本概念，能够保持欧几里得空间内的拓扑关系。
仿射变换包括：旋转、平移、缩放和错切。
图4 通过透明度不同的棋盘图案直观展示了变换前后的几何体。

仿射变换的定义

增广矩阵表示

仿射变换的性质

仿射变换在保持几何体的拓扑关系方面具有重要作用，尤其在二维和三维欧几里得空间中应用广泛。

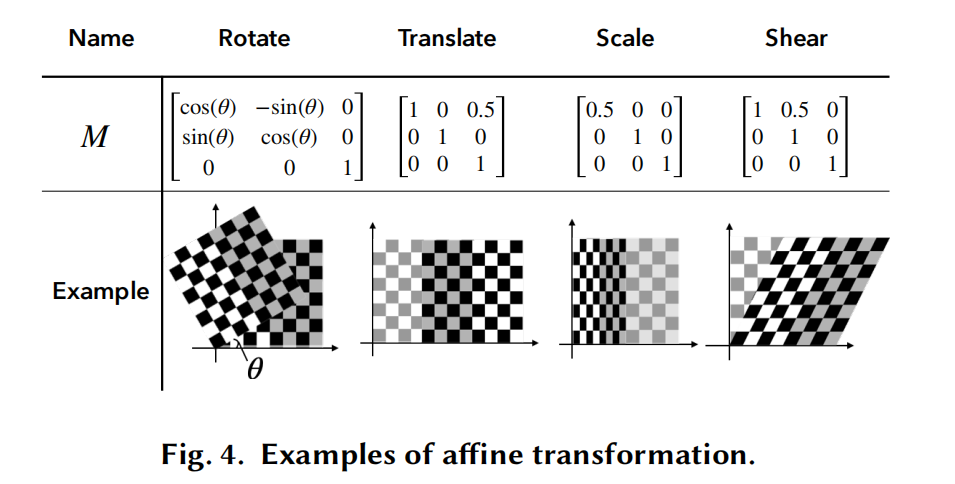
图4展示了仿射变换的四种类型：旋转（Rotate）、平移（Translate）、缩放（Scale）和错切（Shear）。每种变换通过增广矩阵 MMM 表示，并通过示例的棋盘图案直观展示了变换效果。

Affine Equivalent Inputs

直觉的证明

提出命题 3.3：仿射等价几何对的拓扑关系与其原几何对相等。
基于正式拓扑关系的定义（DE-9IM），证明拓扑关系在仿射变换下保持不变。

关键定义

仿射变换（Affine Transformation）：
对单元（cells）的顶点进行变换，保留拓扑特性。
仿射等价几何对（Affine Equivalent Geometry Pairs）：
如果两组几何体可以通过相同的仿射变换 A 相互映射，则它们是仿射等价的。
仿射等价输入（Affine Equivalent Inputs, AEI）：
一个三元组 I=(α,β,Q)，其中 α和 β 是两几何体，Q是拓扑关系查询。如果两个输入满足几何对仿射等价且查询相等，则称其为 AEI。

命题 3.3 证明

非空交集情况：
- 证明 ∂g1∩∂g2 和 ∂g1′∩∂g2′在仿射变换下是一一对应的，且维度保持不变。
空交集情况：
- 通过反证法证明，如果原几何体交集为空，仿射变换后的几何体交集也必为空。

AEI 的应用

根据命题 3.3，若向同一个 SDBMS 提供**仿射等价输入 (AEI)**，则拓扑关系查询的结果应相等。
若结果不一致，则表明 SDBMS 存在逻辑错误。

Spatter

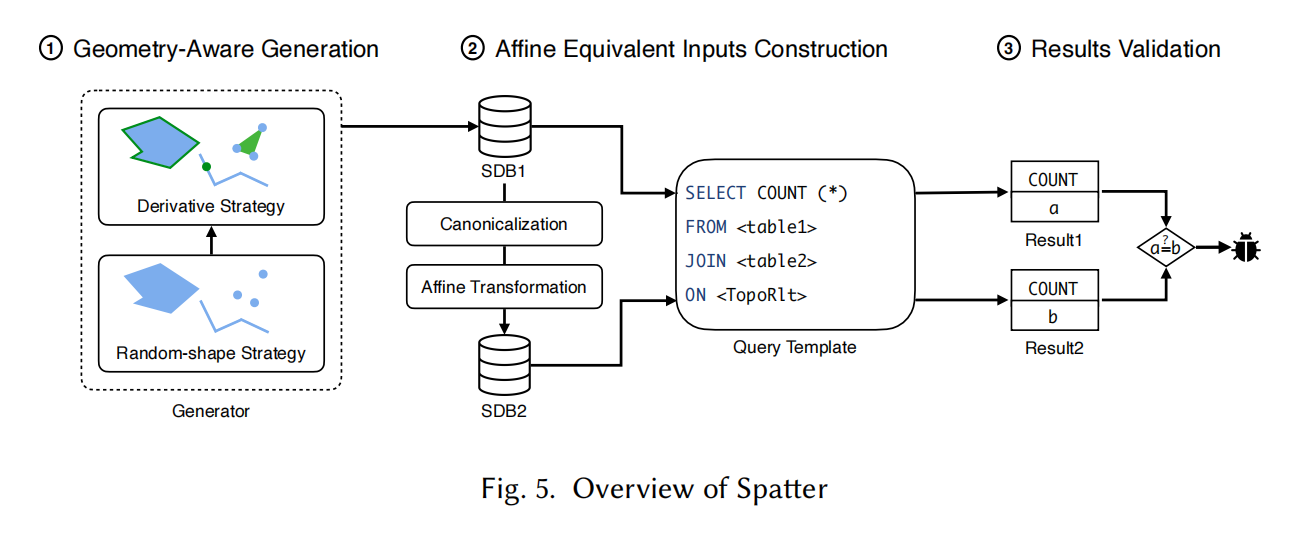
工具简介

Spatter 是一种自动化测试工具，将 AEI 和 几何感知生成器 相结合，用于检测 SDBMS 的逻辑错误。

核心组件

AEI（Affine Equivalent Inputs）：
- 构建两组仿射等价的几何体对，验证它们的拓扑关系是否一致。
几何感知生成器：
- 包括两种策略：
  - 随机形状策略：生成随机几何体。
  - 导出策略：通过对已有几何体应用空间函数来生成新的几何体。
- 优势：在有限数量的几何体中生成多样化的拓扑关系，从而高效地支持 AEI 进行验证。

Spatter 的工作流程

Step 1：
- 使用几何感知生成器生成包含 N 个几何体的数据库 SDB1，包括随机和导出策略。
Step 2：
- 将 SDB1 中的几何体规范化，得到等价表示，然后施加仿射变换，生成新的数据库 SDB2。
- 仿射变换保证拓扑关系不变，规范化确保几何体在空间级别等价。
Step 3：
- 在 SDB1 和 SDB2 上运行同一查询，随机填充查询的占位符，比较返回的行数。
- 若两者结果不一致，则检测到一个逻辑错误。

工具的关键优势

通过 AEI 和几何感知生成器，Spatter 能高效生成和验证复杂的拓扑关系，自动检测 SDBMS 中的逻辑错误。

4.1 Geometry-Aware Generator

几何感知生成器 (Geometry-Aware Generator)

几何感知生成器是 Spatter 的核心组件，用于高效生成几何体，以检测 SDBMS 中的逻辑错误。

问题与挑战

现有方法（如用户报告和单元测试）缺乏自动化的几何生成器。
随机形状策略虽然能生成语法上有效的几何体，但无法涵盖多样的拓扑关系，效率较低。
解决方案：需要生成更多的拓扑关系，同时控制几何体数量，避免过高的时间开销。

两种几何生成策略

随机形状策略（Random-Shape Strategy）
- 原理：随机选择一个几何类型，按其语法定义生成几何体。
- 缺陷：
  - 生成的几何体仅在语法层面有效，可能在语义层面无效（如自相交多边形）。
  - 无效几何会被 SDBMS 报错，Spatter 会忽略这些错误。
导出策略（Derivative Strategy）
- 原理：基于现有几何体，使用 SDBMS 提供的编辑函数导出新几何体。
- 过程：
  - 随机选择 k 个现有几何体。
  - 使用编辑函数生成新的几何体。
  - 若函数不适用，生成一个EMPTY 几何体以处理失败情况。
- 优势：能够有效生成多样化的拓扑关系。

生成过程 (Generation Process)

输入：指定几何体数量 N 和目标表数 m。
步骤：
1. 初始化 m 个空表（数据库 sdb）。
2. 使用随机形状策略生成初始几何体。
3. 逐次生成几何体，随机选择随机形状或导出策略插入到表中。
4. 返回包含生成几何体的数据库 sdb。

编辑函数分类

根据输入几何的维度分类：
- 通用函数：适用于任意维度。
- 维度特定函数：
  - 线段类（Line-based）。
  - 多边形类（Polygon-based）。
  - 多维类（MULTI 和 MIXED 几何体）。

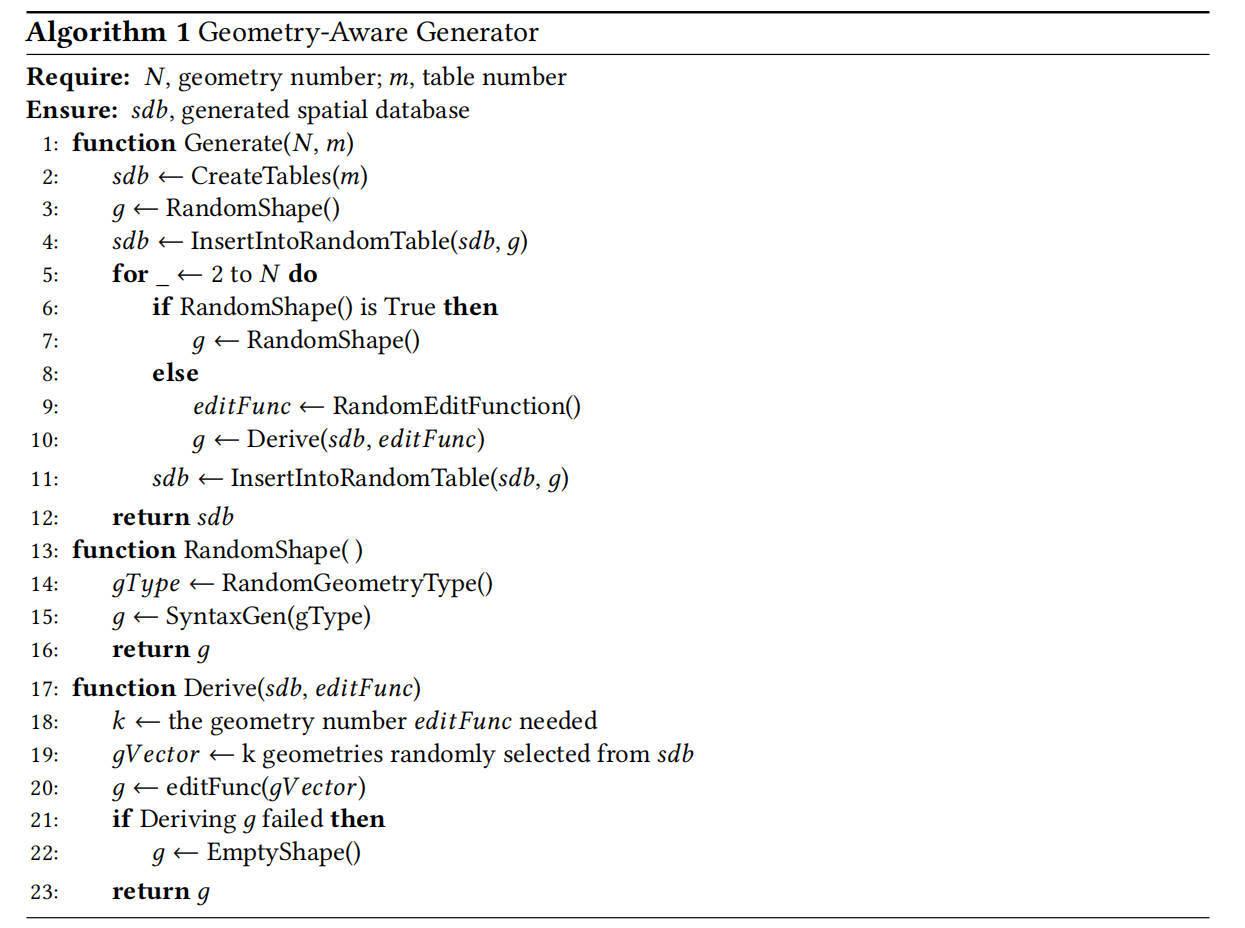
4.2 Affine Transformation

仿射变换的实现

目标：根据命题 3.3，仿射变换保持几何体的拓扑关系。
方法：
1. 输入几何体 g 和欧几里得空间维度 n。
2. 生成映射矩阵 M，其中包括一个可逆矩阵 A 和平移向量 b。
3. 对几何体 g 的每个点 p，通过以下步骤执行仿射变换：
  - 将点 p 转换为齐次向量。
  - 使用矩阵 M 左乘该向量。
  - 将结果向量转换回坐标点。
4. 返回经过变换后的几何体 g′，即仿射等价几何体。

避免精度问题

问题：仿射变换中涉及浮点数运算，容易引入精度误差。
- 示例：理论上 0.1×0.2=0.02，但计算机中结果可能是 0.02+4E−180.02 + 4E-180.02+4E−18。
- 这种误差会导致逻辑错误（例如 PostGIS 的 Listing 1 中的精度问题）。
解决方案：
- 在仿射变换和空间数据生成中，避免使用浮点数。
- 矩阵 A 和向量 b 采用随机整数生成，确保结果不受浮点数精度误差影响。

总结

仿射变换通过可逆矩阵 A 和平移向量 b 构造仿射等价几何体，同时保持拓扑关系。
为避免浮点数精度问题，仿射变换使用整数运算，确保测试结果的可靠性。

4.3 Canonicalization

Canonicalization（规范化）

概念：将几何体的表示转换为规范化表示。
- 规范化被视为构建仿射等价几何体的特殊情况，因为它应用了特殊矩阵 E（返回原几何体）。
- 作用：
  - 构建另一种用于测试的预期结果。
  - 为仿射变换（Algorithm 2）提供预处理方法。

两种规范化级别

元素级别（Element Level）
- 适用于 MULTI 和 MIXED 几何体。
- 过程：
  1. EMPTY 移除：删除几何体中的空元素。
  2. 同质化：将包含单一元素的 MULTI 几何体转换为基本类型，展平嵌套集合。
  3. 去重：删除重复元素（基于形状判断）。
  4. 重新排序：按维度对元素进行排序。
- 示例：
  - 对一个 MULTILINESTRING 进行规范化：
    - 移除 EMPTY，转换为 LINESTRING（单一元素）。
值级别（Value Level）
- 适用于基本类型的几何体：POINT、LINESTRING 和 POLYGON。
- 过程：
  1. 连续去重：删除重复的连续点。
  2. 重新排序：根据坐标值确定顺序：
    - LINESTRING：比较端点坐标，按 x、y、z 顺序判断是否需要反转。
    - POLYGON：将所有闭合环转换为顺时针方向。
- 示例：
  - 对一个 LINESTRING进行规范化：
    - 去除冗余点，重新排序坐标点，确保表示一致。

总结

元素级别规范化：处理 MULTI 和 MIXED 几何体，移除 EMPTY、同质化、去重并排序元素。
值级别规范化：处理基本类型几何体，通过去除冗余点和重新排序坐标，确保表示一致。
作用：提供规范化表示，支持高效的仿射变换与测试验证。

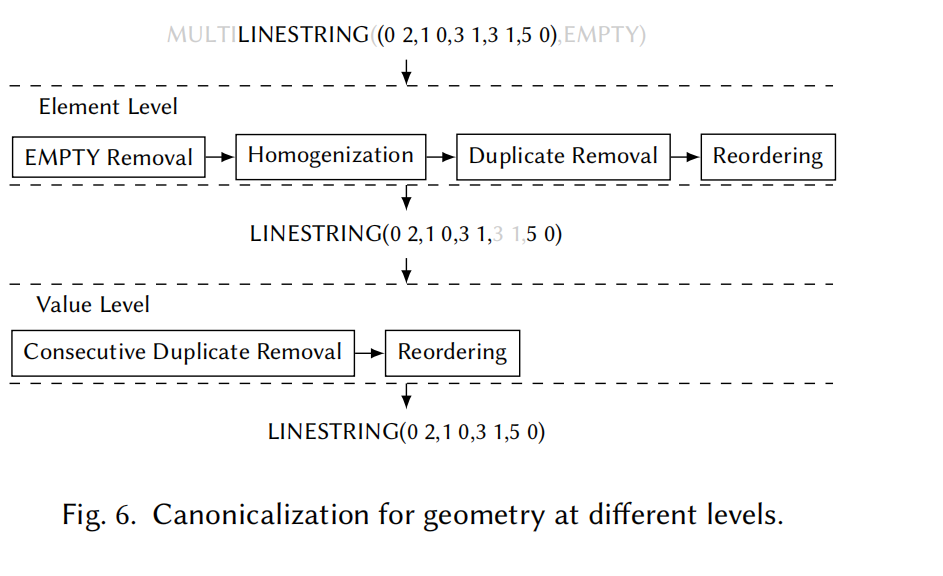
4.4 Results Validation

结果验证（Results Validation）

通过规范化和仿射变换，构建多组仿射等价输入（AEI），用于验证 SDBMS 的结果一致性。

过程描述

构建 AEI 数据库：
- 对空间数据库 SDB1的每个几何体 g，进行：
  - 规范化：生成几何体的规范化表示。
  - 仿射变换：生成仿射等价几何体 g′。
- 构建新的数据库 SDB2，其中 g′存储于与 SDB1 相同的表名中。
查询模板：
- 查询包含三个占位符：
  1. 表名占位符 <table1> 和 <table2>：随机选择 SDB1 中的两个有效表。
  2. 拓扑关系条件占位符 <TopoRlt>：从 SDBMS 用户手册中选择有效的拓扑关系条件（如 ST_Covers）。
- 生成的查询用于从 SDB1 和 SDB2 检索结果。
结果验证：
- 比较相同查询在 SDB1 和 SDB2 上返回的行数。
- 若结果不一致，则表明测试的 SDBMS 存在逻辑错误。

示例

查询：假设 t1 和 t2 是 SDB1 中的两张表，拓扑关系函数为 ST_Covers。
功能：查询 ST_Covers(t1.g, t2.g) 检索 t1 中几何体是否覆盖 t2 中几何体的行数。
验证：若 SDB1 和 SDB2返回的行数不一致，则检测到一个潜在逻辑错误。

总结

通过 AEI 数据库（SDB1和 SDB2）和查询结果对比，验证 SDBMS 是否正确处理拓扑关系。结果不一致表明系统可能存在逻辑错误。

Evaluation

Q1 ：对检测到的错误进行分类并总结，包含开发者反馈。
Q2 ：分析 AEI 发现的错误示例及诱因模式。
Q3 ：评估现有方法是否能发现 AEI 检测的逻辑错误。
Q4 ：展示 Spatter 的测试效率。

测试的 SDBMSs

共测试了 4 个成熟且活跃维护的 SDBMS：
1. PostGIS：
  - 受欢迎度高，在 DB-Engines 排名中名列前茅，为主要测试目标。
2. DuckDB Spatial：
  - DuckDB 的空间扩展版本，DuckDB 是流行的嵌入式 OLAP 系统。
3. MySQL：
  - 流行的开源关系型数据库，测试其内置的空间功能。
4. SQL Server：
  - 一个商业 SDBMS，但由于开发者反馈有限，测试未持续，且未考虑其他商业系统。

5.1 New Bugs

方法概述

Spatter 工具在为期四个月的测试活动中用于检测 SDBMS 中的逻辑错误。每次测试运行时间为 10 分钟至 1 小时，快速检测问题。
问题报告流程：
1. 自动和手动减少潜在问题。
2. 根据 SDBMS 文档验证问题是否违反拓扑关系函数定义。
3. 如果发现问题来自第三方库（如 GEOS），直接向相关社区报告。

错误分类

修复的错误：开发者确认并通过修补程序修复的错误。
确认的错误：开发者已确认，但未修复的错误。
未确认的错误：识别的错误，等待开发者确认。
重复的错误：已确认与先前确认的错误原因相同的错误。

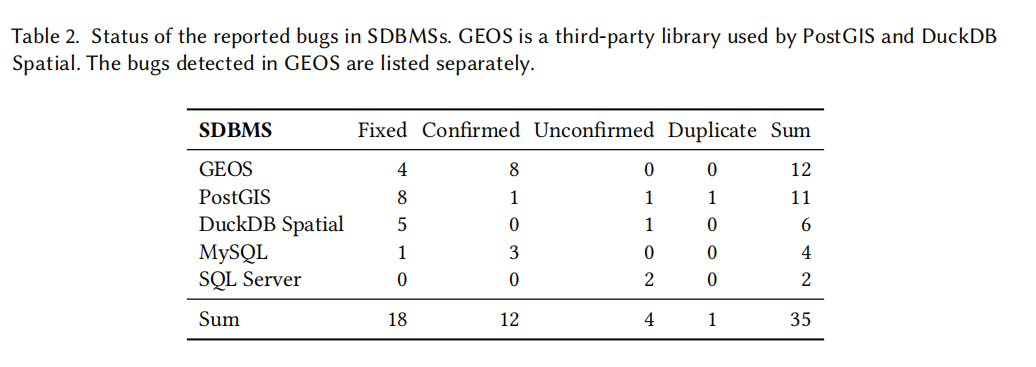
错误检测结果

共检测到 34 个独特的未知错误，其中 30 个已被开发者确认或修复。
错误类型：
- 20 个是逻辑错误，旨在通过 Spatter 查找。
- 9 个 GEOS 的逻辑错误和 7 个 PostGIS 特定的逻辑错误。
- 10 个崩溃错误，所有崩溃错误在一天内得到修复。
逻辑错误比崩溃错误更难修复，通常需要更复杂的根因定位和不影响其他场景的修复。

Spatter 的影响

开发者反馈：
- PostGIS 开发者对 Spatter 的工作表示高度认可，强调其在检测逻辑错误方面的贡献。
- DuckDB Spatial 和 MySQL 的开发者也给予了积极反馈，并在短时间内修复了多个错误。
- 总体而言，Spatter 对 SDBMS 错误检测的工作产生了积极的影响，并帮助开发者发现了新的问题。

5.2 Illustrative Examples

Listing 3: MySQL 缩放后错误的关系计算

问题描述：
- 几何体 @g1 和 @g2被用于测试函数 ST_Crosses。根据定义，ST_Crosses 的条件是两几何体相交且交集不等于任一输入几何体。
- 错误：在缩放坐标后，MySQL 错误地判断 @g1 和 @g2 相交，违反了上述定义。
- 错误原因：MySQL 逻辑在处理包含 EMPTY 元素的几何体时存在问题。
- 检测难点：
  - 由于 SDBMS 对 ST_Crosses 的实现差异大，难以通过差分测试发现这个错误。
- 处理结果：问题已报告给 MySQL 社区。

Listing 4: MySQL 交换坐标轴后错误的关系计算

问题描述：
- 几何体 @g1 和 @g2 被用于测试函数 ST_Overlaps。函数定义如下：
  - 若 g1 和 g2 相交，且交集的维度与输入相同但不等于任一输入几何体，则返回 1；否则返回 0。
- 错误：
  - 在此测试中，g1 的交集等于 g1，因此预期结果为 0，但 MySQL 返回了错误结果 1。
- 特殊性：
  - PostGIS 和 DuckDB Spatial 将 g2g判定为无效几何体（因其元素相交，导致自相交错误）。
- 检测难点：
  - 不同 SDBMS 的数据设计差异会限制差分测试的有效性。
- 处理结果：此错误已被确认为 MySQL 的逻辑错误。

Listing 5: PostGIS 计算距离的 EMPTY 元素相关 Bug

问题描述：
- 测试函数ST_Distance，其定义为计算两个几何体 g1 和 g2的最小距离：
  - 如果输入是 MULTI 几何体，则返回所有点对之间的最小距离。
- 错误：
  - 对于 MULTIPOINT 几何体，预期结果为 2，但 PostGIS 错误地返回了 3。
- 错误原因：
  - 递归逻辑存在问题，导致错误结果。
- 检测方式：
  - 此 Bug 是通过规范化 (Canonicalization) 检测到的。
- 处理结果：PostGIS 开发者已修复该问题。

总结

Listing 3 和 Listing 4 的问题：逻辑错误由几何函数的不一致实现或定义引起，且差分测试难以发现。
Listing 5 的问题：涉及 EMPTY 元素的处理问题，通过规范化成功发现。
影响：这些错误展示了在几何关系计算中，SDBMS 的实现细节和边界条件处理可能导致的逻辑问题。

Listing 6: PostGIS 在 MIXED 几何体边界计算中的错误策略

问题描述：
- 测试函数 ST_Within(g1, g2)，定义如下：
  - 当且仅当 g1 的内部完全包含在 g2 的内部时，返回 TRUE。
- 在测试中：
  - g1 是 POINT(0 0)。
  - g2 是一个 GEOMETRYCOLLECTION，包含 POINT(0 0) 和 LINESTRING(0 0, 1 0)。
  - 两个几何体的内部共享点 POINT(0 0)，因此 g1 应该在 g2 内，预期结果为 TRUE。
错误：PostGIS 错误地返回 FALSE，没有正确判断两几何体的关系。
错误原因：
- PostGIS 使用了 GEOS 的 “last-one-wins” 策略：
  - GEOMETRYCOLLECTION 的最后一个几何体（此处为 LINESTRING）的边界优先级较高。
  - 结果是 POINT(0 0) 被认为是边界的一部分，而不是 g2 的内部。
检测方法：
- 此 Bug 可通过差分测试检测：PostGIS 和 MySQL 返回不同结果（PostGIS 错误，而 MySQL 正确）。
- 但若与 DuckDB Spatial 对比，此 Bug 难以发现，因为两者都返回错误结果。
开发者反馈：
- 开发者确认此问题是 GEOS 的上游 Bug，提出改用边界优先级语义（boundary-priority semantics）进行修复。

Listing 7: PostGIS 在预处理几何体 (Prepared Geometry) 中遗漏了一对结果

问题描述：
- 测试函数 ST_Contains(g1, g2)，定义如下：
  - 当且仅当 g1 包含 g2，且 g2 的所有点都位于 g1 的内部，并且 g1 和 g2 的内部共享至少一个点时，返回 TRUE。
- 在测试中：
  - 第三个几何体 MULTIPOLYGON 应包含第二个几何体 MULTIPOINT，但 PostGIS 错误地遗漏了 (3,2) 这一对 id 结果，只返回 (3,1)。
错误原因：
- 问题出在 GEOS 的 “prepared geometry” 组件，该组件用于加速拓扑关系函数的计算。
- “Prepared Geometry” 的逻辑与未优化的逻辑结果不一致，导致部分配对被遗漏。
检测方法：
- 此 Bug 可通过差分测试检测：PostGIS 返回错误结果，而 MySQL 和 DuckDB Spatial 返回正确结果。
开发者反馈：
- PostGIS 开发者将此 Bug 归因于 GEOS 的上游问题，并反馈称这种不一致可能在 PostGIS 中更为普遍。
- Bug 在确认后一天内被修复。

Listing 8: PostGIS 引擎中 GIST 索引导致的逻辑错误

问题描述：
- 测试在表 t 中查找与 POINT EMPTY 匹配的记录。
- 使用了 GIST 索引 并禁用了顺序扫描（enable_seqscan = false）。
- 预期结果为 1，因为表中存在 POINT EMPTY，但 PostGIS 错误地返回了 0。
错误原因：
- GIST 索引的实现存在问题，未正确处理 EMPTY 几何体的匹配逻辑。
错误的多样性：
- 此 Bug 是 PostGIS 引擎中检测到的 7 个逻辑错误之一，显示了 PostGIS 在处理索引和几何体时存在潜在的不一致性。
处理结果：
- 此 Bug 已被修复。

Listing 9: PostGIS 中 RANGE 功能的定义问题

问题描述：
- 测试函数 ST_DFullyWithin，其定义为：
  - 如果两个几何体在指定的距离范围内完全包含，则返回 TRUE。
- 在测试中：
  - 几何体 LINESTRING(0 0,1 1,0 0) 应完全包含在距离 100 的 POLYGON 范围内，因此预期结果为 TRUE。
  - 但 PostGIS 错误地返回了 FALSE。
错误原因：
- 开发者指出 ST_DFullyWithin 的定义可能存在问题：
  - 当前的实现未能满足用户对函数的正确预期，即检查范围内的完全包含性。
  - 函数逻辑与其名称所传达的含义不一致，可能需要重新定义或重新实现。
开发者反馈：
- 开发者承认定义存在问题，并计划提出新算法来解决此问题。

Bug Classification

Bug 诱因模式分类

将诱发 Bug 的模式归类为 EMPTY 几何体 和 MIXED 几何体 两大类，提供了基于触发案例模式的 Bug 分类法。

逻辑 Bug 的分布

EMPTY 几何体相关：
- 在 20 个逻辑 Bug 中，有 6 个由包含 EMPTY 元素或几何体 的测试案例触发。
- 修复难度：这类 Bug 的根因（如空处理器问题）较容易定位，通常能在一天内修复。
MIXED 几何体相关：
- 有 13 个 Bug 与
  
  MIXED 几何体
  
  相关，由多种因素引起：
  1. EMPTY 元素处理错误：4 个 Bug。
  2. 维度处理器问题：3 个 Bug 由于维度处理器错误识别 MIXED 几何体的维度。
  3. “Prepared Geometry” 优化组件问题：检测到 2 个相关逻辑 Bug，涉及 PostGIS 的优化组件。
  4. 边界处理器问题：Listing 6 的 Bug 与 MIXED 几何体的边界处理器错误有关。

总结

EMPTY 几何体 相关 Bug 易修复，原因通常更明显。
MIXED 几何体 相关 Bug 更复杂，涉及维度处理器、边界处理器以及优化组件等不同环节的问题。
提出的分类法有助于快速定位不同类别的 Bug 根因并提供针对性修复方法。

5.3 Comparison to the State of the Art

对比现有方法

Spatter 的独特性：
- Spatter 是首个通用的测试工具和方法，专门用于检测 SDBMS 中的逻辑错误。
- 为验证 AEI 检测 Bug 的独特性，进行了与现有方法的比较分析。

比较方法

差分测试：
- 比较不同 SDBMS 的输出：
  - PostGIS vs. DuckDB Spatial（相似系统）。
  - PostGIS vs. MySQL（不同系统）。
- 比较同一 SDBMS 中的索引开关状态（Index 方法）。
TLP 方法：
- 将每个诱发 Bug 的查询分解为三个分区查询，检查是否出现意外结果。

结果分析

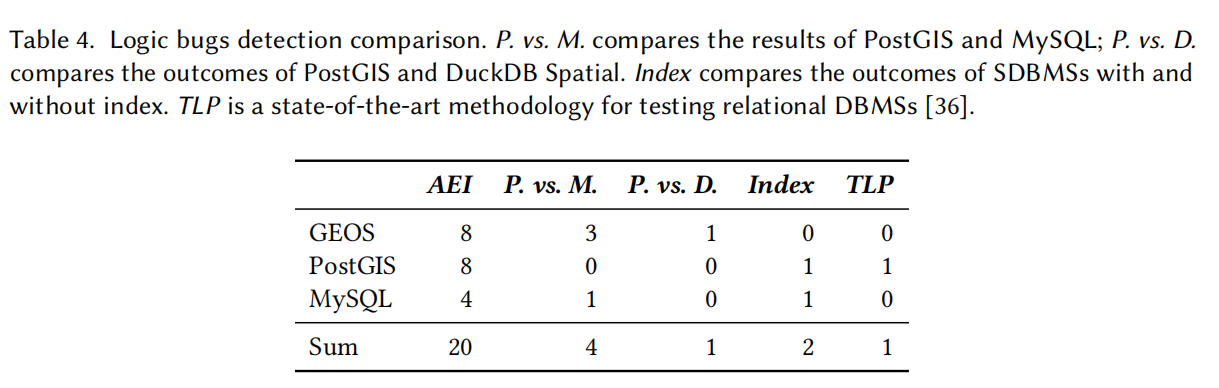
总计 20 个逻辑错误：
- 14 个逻辑错误：所有现有方法都未能检测到。
- 4 个逻辑错误：可通过 PostGIS 和 MySQL 的差分测试检测，但差分测试容易因函数定义差异导致误报。
- 0 个逻辑错误：PostGIS 与 DuckDB Spatial 的比较中未检测到任何错误，因两系统过于相似。
- 2 个索引相关错误：可通过 Index 方法检测，但依赖测试案例设计，需频繁使用索引才能高效应用。
- 1 个索引相关错误：TLP 方法检测到，但 TLP 缺乏对空间关系的认知，无法检测其他逻辑错误。

总结

Spatter 能有效检测大多数逻辑错误，而现有方法（差分测试、TLP 等）在空间关系逻辑 Bug 上表现有限。
差分测试存在误报，且系统相似性限制了其有效性；TLP 方法缺乏对空间关系的处理能力。
Spatter 的 AEI 方法显著提升了 SDBMS 中逻辑错误的检测能力。

这部分的实验是怎么做到呢？存不存在随机性因素

5.4 Efficiency of Spatter

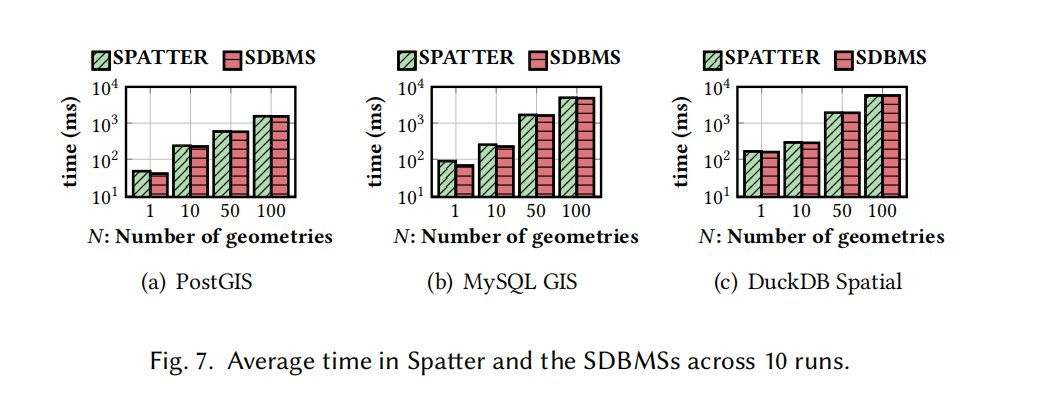
运行时间分布

方法：
- 测试几何体数量 (N) 的影响，分别设置为 1、10、50、100，并运行 100 个随机查询，每种配置重复 10 次。
结果：
- 当 N>10时，SDBMS 的执行时间占总运行时间的 90%以上。
- N 增加时，Spatter 的总运行时间显著增加，尤其是在 DuckDB Spatial 和 MySQL 中，当 N=100 时运行时间比 N=10长 20 倍。
- 执行时间主要由 SDBMS 执行消耗主导，测试效率受到几何体数量的间接影响。
- 请注意，Spatter的执行时间还包括在SDBMS中花费的时间

代码覆盖率

方法：
- 在 PostGIS 上运行 Spatter 超过 24 小时，收集 PostGIS 和 GEOS 的行覆盖数据。
- 比较单元测试与 “单元测试 + Spatter” 的覆盖率，分析 Spatter 对额外覆盖的贡献。
结果：
- PostGIS 和 GEOS 的覆盖率分别增加 206 和 178 行代码，表明 Spatter 补充了单元测试的覆盖范围。
- 总覆盖率较低（PostGIS < 20%，GEOS ~20%），因 Spatter 专注于拓扑关系查询而非其他功能（如 I/O 或空间操作）。

随机形状策略基线测试

方法：
- 设计基线生成器，仅使用随机形状策略，评估与几何感知生成器（结合导出策略）的效率差异。
- 在 PostGIS 上运行 1 小时，记录触发 Bug 的案例数量、检测时间和代码覆盖率。
结果：
- 几何感知生成器检测到的独特 Bug 数量显著高于随机形状策略，因导出策略生成了更复杂的拓扑关系。
- 几何感知生成器在 PostGIS 和 GEOS 中达到更高的代码覆盖率，利用了 PostGIS 的空间函数。

总结

运行效率：SDBMS 的执行时间占据主要成本，几何体数量对总运行时间有显著影响。
代码覆盖：Spatter 补充了单元测试的覆盖范围，尤其是在拓扑关系查询模块中。
测试效率：结合导出策略的几何感知生成器在检测 Bug 和覆盖范围方面显著优于随机形状策略。
意义：导出策略通过基于现有几何体创建新几何体，提高了测试效率和覆盖率，增强了 Spatter 在 SDBMS Bug 检测中的表现。

Discussion

AEI 检测 Bug 的原因

机制：AEI 通过对比原始输入和变换后的数据库，触发程序中的不同执行路径，从而发现 Bug。
实例：
- Listing 1 的 Bug：由于点 ppp 的方向计算中精度丢失导致错误，但 Listing 2 的点位于原点，因此未触发该 Bug。
- Listing 5 的 Bug：由 MULTI 几何体的递归处理逻辑错误引起，但递归逻辑未被第二个几何体调用。
总结：AEI 通过变换后的不同路径有效检测出多种 Bug。

支持的 SDBMS 功能

JOIN 功能：测试所有案例中均包含空间数据 JOIN，因其是 SDBMS 的核心功能之一。
RANGE 功能：测试函数包括 ST_Within、ST_DWithin 和 ST_DFullyWithin，并发现了显著 Bug（如 Listing 9）。
总结：AEI 能有效测试与几何体相关的功能，如拓扑关系查询。

扩展到其他数据库系统的适用性

KNN 算法：AEI 的核心方法可用于测试支持 KNN（最近邻搜索）的系统（如向量数据库系统）：
1. 生成数据库 SDB1。
2. 对几何体进行规范化和仿射变换，构造 SDB2。
3. 检查 SDB1 和 SDB2 的 KNN 结果是否一致。
- 限制：剪切变换不适用，因为它破坏了相对距离属性。

AEI 的局限性

不支持地理类型：地理类型（如曲面对象）不适用于仿射变换。
不适用于文件读取与转换：AEI 不能检测如 GDAL 库中的文件处理 Bug（如 DuckDB Spatial 无法正确解析空 GeoJSON）。
不适用于非线性变换或非仿射几何操作：例如，ST_Buffer 在仿射变换后无法保持拓扑关系。

未来工作

扩展到几何库：直接应用 AEI 测试几何库（如 PostGIS 的 Bug 中 12 个源自几何库）。
引入符号执行：使用符号执行探索更多执行路径，AEI 提供预期结果替代几何生成器。
推广到其他 DBMS：将 AEI 的核心思想（保留基本属性的数据库变换）扩展到其他数据库系统，例如图数据库（GDBMS）。

总结

AEI 在 SDBMS 中检测逻辑错误方面具有显著优势，未来工作将探索 AEI 在几何库、符号执行和其他 DBMS 系统中的潜力，同时克服其地理类型和非线性变换的局限性。

Finding Logic Bugs in Spatial Database Engines via Affine Equivalent Inputs

Abstract

INTRODUCTION

Background

2.1 Geometry Types

2.2 Topological Relationship Queries

正式拓扑关系 (Formal Topological Relationships)

示例：ST_Relate

2. 命名拓扑关系 (Named Topological Relationships)

示例：ST_Intersects 和 ST_Covers

2.3 Affine Transformations

Affine Equivalent Inputs

Spatter

4.1 Geometry-Aware Generator

4.2 Affine Transformation

4.3 Canonicalization

4.4 Results Validation

Evaluation

5.1 New Bugs

5.2 Illustrative Examples

Bug Classification

5.3 Comparison to the State of the Art

5.4 Efficiency of Spatter

Discussion